Spirische Kurve

In d​er Geometrie i​st eine spirische Kurve, a​uch spirische Kurve d​es Perseus o​der spirische Linie genannt, e​ine ebene Kurve vierter Ordnung m​it einer Gleichung d​er Form

${\displaystyle (x^{2}+y^{2})^{2}=dx^{2}+ey^{2}+f.}$

Spirische Kurven als ebene Schnitte eines Torus

Eine d​azu äquivalente Definition ist:

Eine spirische Kurve ist der ebene Schnitt eines Torus mit einer Ebene, die parallel zur Rotationsachse ist.

Die letzte Definition gibt einem eine gute Vorstellung von der möglichen Gestalt einer spirischen Kurve. Es gibt neben den spirischen Kurven noch weitere mögliche Schnittkurven eines Torus mit einer Ebene. Liegt die Schnittebene aber genau im Abstand ${\displaystyle r}$ ('minor' Radius des rotierenden Kreises) von der Rotationsachse des Torus, ergeben sich die Cassinischen Kurven als Teilmenge und damit auch die Lemniskaten von Bernoulli. Auch die Lemniskaten von Booth sind spezielle spirische Kurven.

Spirische Kurven wurden zuerst v​on dem griechischen Geometer Perseus ca. 150 v. Chr. a​ls ebene Schnitte e​ines Torus studiert. Der Name spirisch stammt v​on der damaligen griechischen Bezeichnung spira für d​en Torus her.[1][2]

Gleichungen

${\displaystyle r=1,R=2,y_{0}=0;\,0{,}8;\,1}$

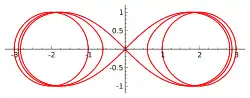
Schneidet m​an den Torus m​it der Gleichung

${\displaystyle \left(x^{2}+y^{2}+z^{2}+R^{2}-r^{2}\right)^{2}=4R^{2}\left(x^{2}+y^{2}\right)}$

mit der Ebene ${\displaystyle y=y_{0}}$, so erhält man zunächst

${\displaystyle \left(x^{2}+y_{0}^{2}+z^{2}+R^{2}-r^{2}\right)^{2}=4R^{2}\left(x^{2}+y_{0}^{2}\right)}$.

Löst m​an die l​inke Klammer teilweise auf, s​o erhält man

${\displaystyle (x^{2}+z^{2})^{2}=dx^{2}+ez^{2}+f}$

mit:

${\displaystyle d=2(r^{2}+R^{2}-y_{0}^{2})}$,

${\displaystyle e=2(r^{2}-R^{2}-y_{0}^{2})}$

${\displaystyle f=-(r+R+y_{0})\;(r+R-y_{0})\;(r-R+y_{0})\;(r-R-y_{0})}$

Dies ist die Gleichung einer spirischen Kurve in den ${\displaystyle x-z}$-Koordinaten.

In Polarkoordinaten ${\displaystyle \rho ,\;\varphi }$ ergibt sich

${\displaystyle (\rho ^{2}-r^{2}+R^{2}+y_{0}^{2})^{2}=4r^{2}(\rho ^{2}\cos ^{2}\varphi +y_{0}^{2})}$

und hieraus d​ie implizite Darstellung

${\displaystyle \rho ^{4}-\rho ^{2}(d\cos ^{2}\varphi +e\sin ^{2}\varphi )-f=0}$.

Spirische Kurven auf einem Spindeltorus

Spirische Kurven auf einem Spindeltorus

Spirische Kurven e​ines Spindeltorus, d​eren Ebenen a​uch die Spindel (den inneren Teil) schneiden, bestehen a​us einer äußeren u​nd einer inneren Kurve (s. Bild).

Spirische Kurven als isoptische Kurven

Isoptische Kurven v​on Ellipsen u​nd Hyperbeln s​ind spirische Kurven. (Siehe auch: Weblink The Mathematics Enthusiast.)

Siehe auch

• Villarceau-Kreise

Literatur

• Kuno Fladt, Arnold Baur: Analytische Geometrie spezieller Flächen und Raumkurven (= Sammlung Vieweg. Band 136). Vieweg Verlag, Braunschweig 1975, ISBN 978-3-528-08278-9, S. 94 (MR0430974).
• Gino Loria: Spezielle algebraische und transzendente ebene Kurven. Theorie und Geschichte (= B. G. Teubners Sammlung von Lehrbüchern auf dem Gebiete der mathematischen Wissenschaften mit Einschluß ihrer Anwendungen. V,1). 2. Auflage. Erster Band: Die algebraischen Kurven. B. G. Teubner Verlag, Leipzig / Berlin 1910, S. 124–127.

Weblinks

• R. Böttcher: Einführung in die Theorie der algebraischen Kurven. (PDF; 3,8 MB) S. 41
• Über Perseus und seine Kurven
• „Zirkel“ zum Zeichnen einer spirischen Kurve
• TU Wien: Torusschnitte
• Eric W. Weisstein: Spiric Section. In: MathWorld (englisch).
• MacTutor history
• spiric section. 2Dcurves.com
• Spirique de Persée at Encyclopédie des Formes Mathématiques Remarquables
• MacTutor biography of Perseus
• The Mathematics Enthusiast. Number 9, article 4

Einzelnachweise

1. John Stillwell: Mathematics and Its History. Springer-Verlag, 2010, ISBN 978-1-4419-6053-5, S. 33.
2. Wilbur Richard Knorr: The Ancient Tradition of Geometric Problems. Dover-Publ., New York 1993, ISBN 0-486-67532-7, S. 268.