Shakersort
Der Begriff Shakersort bezeichnet einen stabilen Sortieralgorithmus, der eine Menge von linear angeordneten Elementen (z. B. Zahlen) der Größe nach sortiert. Weitere Namen für diesen Algorithmus sind Cocktailsort, Ripplesort, Shearsort oder BiDiBubbleSort (bidirektionales Bubblesort).
Prinzip
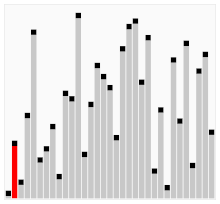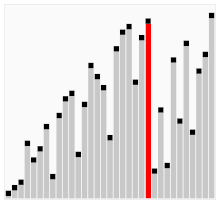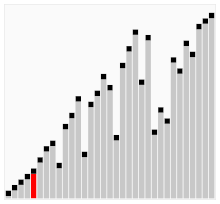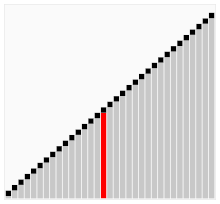
Das zu sortierende Feld wird abwechselnd nach oben und nach unten durchlaufen. Dabei werden jeweils zwei benachbarte Elemente verglichen und gegebenenfalls vertauscht.
Durch diese Bidirektionalität kommt es zu einem schnelleren Absetzen von großen bzw. kleinen Elementen. Anhand des Sortierverfahrens lässt sich auch der Name erklären, denn der Sortiervorgang erinnert an das Schütteln des Arrays oder eines Barmixers.
Komplexität
Der Algorithmus besitzt eine quadratische und daher im Vergleich zu vielen anderen Sortieralgorithmen schlechte Worst-Case-Laufzeit, die jedoch in der einfachen Version gleichzeitig auch der normalen Laufzeit entspricht. In der Informatik drückt man dies mittels Landau-Symbol durch aus. Dafür bietet dieser Algorithmus den Vorteil eines geringen Speicherbedarfes. Da der Algorithmus ein In-place-Verfahren ist, braucht er keinen zusätzlichen Speicher. Zudem hat Shakersort auf fast sortierten Arrays eine lineare Laufzeitkomplexität ().
Formaler Algorithmus
Der Algorithmus sieht im Pseudocode folgendermaßen aus. Das erste Element der Liste sortierbarer Elemente A hat hierbei den Index 0:
prozedur shakerSort( A : Liste sortierbarer Elemente ) beginn := -1 ende := Länge( A ) - 2 wiederhole vertauscht := falsch beginn := beginn + 1 für jedes i von beginn bis ende wiederhole falls A[ i ] > A[ i + 1 ] dann vertausche( A[ i ], A[ i + 1 ] ) vertauscht := wahr ende falls ende für falls vertauscht = falsch dann brich wiederhole-solange-Schleife ab ende falls vertauscht := falsch ende := ende - 1 für jedes i von ende bis beginn wiederhole falls A[ i ] > A[ i + 1 ] dann vertausche( A[ i ], A[ i + 1 ] ) vertauscht := wahr ende falls ende für solange vertauscht prozedur ende
Beispiel
Eine Reihe von sechs Zahlen soll aufsteigend sortiert werden. Die fett markierten Zahlenpaare werden verglichen. Wenn die rechte Zahl hierbei kleiner ist als die linke, so werden die Zahlen vertauscht (blau markiert).
55 07 78 12 42 33 1. Durchlauf 07 55 78 12 42 33 07 55 78 12 42 33 07 55 12 78 42 33 07 55 12 42 78 33 07 55 12 42 33 78 2. Durchlauf 07 55 12 33 42 78 07 55 12 33 42 78 07 12 55 33 42 78 07 12 55 33 42 78 3. Durchlauf 07 12 55 33 42 78 07 12 33 55 42 78 07 12 33 42 55 78 4. Durchlauf 07 12 33 42 55 78 07 12 33 42 55 78 5. Durchlauf 07 12 33 42 55 78 Fertig sortiert.