Sechsecksatz von Catalan

Der Sechsecksatz von Catalan ist ein Lehrsatz der Elementargeometrie, welcher folgendes besagt:[1]

In einem Sechseck[2] der euklidischen Ebene mit Eckpunkten

A,B,C,D,E,F

, dessen drei Diagonalen von gleicher Länge und dessen gegenüberliegende Seiten jeweils parallel sind, welches also

{\overline {AD}}={\overline {BE}}={\overline {CF}}

sowie

{AB}\parallel {DE}

bzw.

{BC}\parallel {EF}

bzw.

{CD}\parallel {FA}

erfüllt, liegen die Eckpunkte

A,B,C,D,E,F

stets auf einem Kreis.

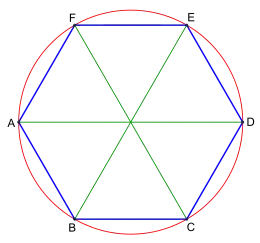
Sechsecksatz von Catalan

Er ist nach Eugène Charles Catalan benannt.

Literatur

Heinrich Dörrie: Mathematische Miniaturen. 2. Auflage. Sändig, Wiesbaden 1979, ISBN 3-500-21150-X (unveränderter Nachdruck der Ausgabe 1943).

Einzelnachweise und Anmerkungen

Heinrich Dörrie: Mathematische Miniaturen. 2. Auflage. Sändig, Wiesbaden 1979, ISBN 3-500-21150-X, S. 38, 521 (unveränderter Nachdruck der Ausgabe 1943).
Gemeint ist eine konvexe geometrische Figur.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Heinrich Dörrie: Mathematische Miniaturen. 2. Auflage. Sändig, Wiesbaden 1979, ISBN 3-500-21150-X, S. 38, 521 (unveränderter Nachdruck der Ausgabe 1943).

[2] Gemeint ist eine konvexe geometrische Figur.