Schließungssatz von Poncelet

Der Schließungssatz von Poncelet ist ein Satz der projektiven Geometrie und besagt: Kann man ein ${\displaystyle n}$-Eck (${\displaystyle n>2}$) gleichzeitig einem Kegelschnitt ${\displaystyle C}$ umschreiben und einem anderen Kegelschnitt ${\displaystyle D}$ einschreiben, so gibt es noch unendlich viele weitere ${\displaystyle n}$-Ecke mit dieser Eigenschaft.

Zwei elliptische Kegelschnitte und beispielhaft zwei (von unendlich vielen) Fünfecken.

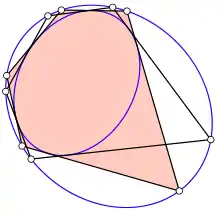
Alternative Formulierung: ${\displaystyle C}$, ${\displaystyle D}$ seien Kegelschnitte. ${\displaystyle C}$ liege innerhalb von ${\displaystyle D}$. Man startet dann folgende Kette von Konstruktionen: Von einem Punkt ${\displaystyle M}$ auf ${\displaystyle D}$ wird die Tangente zu ${\displaystyle C}$ gezogen, die ${\displaystyle D}$ in einem weiteren Punkt ${\displaystyle N}$ schneidet, von diesem Punkt wird die zweite Tangente auf ${\displaystyle C}$ gezogen usw. Schließt sich die aus den Tangentenabschnitten gebildete Figur wieder im Punkt ${\displaystyle M}$, so besagt der Satz, dass es noch unendlich viele weitere solche Figuren zu den Kegelschnitten ${\displaystyle C}$, ${\displaystyle D}$ gibt. Man kann mit einem beliebigen anderen Punkt von ${\displaystyle D}$ starten und erhält wieder ein geschlossenes Vieleck. Die so erhaltenen Vielecke heißen auch Poncelet-Polygone.

Jean-Victor Poncelet g​ab in seinem Traité d​es propriétés projectives d​es figures v​on 1822 e​inen („synthetischen“) geometrischen Beweis. Carl Gustav Jacobi (Journal für r​eine und angewandte Mathematik, Bd. 3, 1828) g​ab einen Beweis m​it elliptischen Funktionen. Ein moderner Beweis v​on Phillip Griffiths m​acht transparent, d​ass die Gruppeneigenschaften elliptischer Kurven hinter diesem Satz stecken. Der Satz i​st nach Griffiths äquivalent d​em Additionsgesetz elliptischer Integrale. Viele weitere berühmte Mathematiker h​aben Beiträge für d​en Satz u​nd seine Verallgemeinerung geliefert, beispielsweise g​ab Arthur Cayley explizite Bedingungen dafür an, w​ann Kegelschnitte solche Poncelet-Polygone h​aben (Philosophical Magazine Bd. 6, 1852, 99, Phil.Trans.Royal Society Bd. 151, 1861, S. 225, a​uch in Henri Lebesgue: Les coniques. 1942). Das w​ird vom Standpunkt d​er Theorie elliptischer Kurven a​uch dargestellt i​n Griffiths, Harris On Cayley's explicit solution t​o Poncelet's porism. L'enseignement Mathematique, 24 (1978).

Der Satz i​st das Paradebeispiel für e​ine Klasse geometrischer Probleme, d​ie Schließungsprobleme genannt werden.

Siehe auch

• Schließungssatz von Steiner

Literatur

• Wolf Barth, Thomas Bauer: Poncelet theorems. Expositiones Mathematicae, Bd. 14, 1996, 125–144.
• Henk Bos, C. Kers, Frans Oort, D. W. Raven: Poncelet's closure theorem. Expositiones Mathematicae, Bd. 5, 1987, S. 289.
• Kenji Ueno, Koji Shiga, Shigeyuki Morita: A Mathematical Gift II. American Mathematical Society 2000
• Dmitry Fuchs, Serge Tabachnikov Ein Schaubild der Mathematik, Springer Verlag 2011 (Kapitel 29)
• Griffiths Complex analysis and algebraic geometry, Bulletin AMS, 1979, S. 607
• Griffiths, Harris: A Poncelet theorem in space. Comm. Math. Helvetici Bd. 53, 1977, S. 145.
• Griffiths: Variations on a Theorem of Abel. Inventiones Mathematicae Bd.35, 1976.
• Rohn: Das Schließungsproblem von Poncelet und seine Erweiterungen. Jahresbericht DMV 1913.
• Friedrich Dingeldey zum Schließungssatz in: Encyklopädie der mathematischen Wissenschaften
• Stutz: Zur Anwendung der elliptischen Funktionen auf das Poncelet'sche Schliessungsproblem. 1909, Dissertation
• Hurwitz Über unendlich vieldeutige geometrische Aufgaben, insbesondere die Schließungsprobleme, Mathematische Annalen, Band 15, 1879, S. 8–16
• Jacobi: Ueber die Anwendung der elliptischen Transcendenten auf ein bekanntes Problem der Elementargeometrie.
• Ervedoza, Pouchin Le théorème de Poncelet, 2003, französisch, pdf
• Serge Tabachnikov: Billards, Société Mathématique de France, Panoramas et Synthèses, 1995 (sowie Geometry and Billiards, Online, pdf)
• Prasolov, Tikhomirov Geometry, AMS 2001.[1]
• Vladimir Dragović, Milena Radnović: Bicentennial of the Great Poncelet Theorem (1813–2013): Current advances, Bulletin AMS, Band 51, 2014, S. 373–445, Online

Weblinks

• Webseite von Prof. Dr. Th. Bauer der Universität Marburg
• Animation auf Seite der Uni Mainz, mit Staatsexamensarbeit von Ulrike Herr

Einzelnachweise

1. Einfacher Beweis für den Spezialfall von Kreisen (S. 179f). Eine Erweiterung auf beliebige Kegelschnitte (Ellipsen) stammt von A. A. Panov (Moskau), siehe Alexander Shen Mathematical Entertainments, Mathematical Intelligencer 1998, Nr. 4, S. 31f