Schild-Plot

Der Schild-Plot ist ein nach Heinz Otto Schild benanntes grafisches Verfahren zur Ermittlung der pharmakologischen Wirkpotenz eines Antagonisten (pA₂-Wert) unter Nutzung der Linearen Regression (Schild-Regression).[1] Der Schild-Plot beschreibt dabei den linearen Zusammenhang zwischen dem Logarithmus der molaren Antagonistenkonzentration (log [Antagonist]) und der Hemmwirkung des Antagonisten (dargestellt als log (r-1)):

\operatorname {p} A_{2}=-\log \,[Antagonist]+\log \,(r-1)

Besondere Bedeutung besitzt die Regressionsgerade im Schild-Plot. Ihre Steigung liefert Aussagen über die Art des Antagonismus. Die antagonistische Potenz (pA₂-Wert) entspricht dem Abszissenschnittpunkt der Regressionsgeraden.

Praktische Durchführung

Zur Aufnahme eines Schild-Plots und zur daraus folgenden Berechnung des pA₂-Werts wird der Antagonist in getrennten Experimenten in unterschiedlichen Konzentrationen in einem pharmakologischen Testsystem (z. B. Zellkultur oder Gewebe) inkubiert oder, bei Tierversuchen, einem Versuchstier verabreicht. Anschließend wird durch Zugabe bzw. Verabreichung steigender Konzentrationen eines Agonisten üblicherweise die Agonistenkonzentration ermittelt, bei der ein halbmaximaler Effekt beobachtet werden kann (EC₅₀-Wert). Dieser Wert ist von der Konzentration des Antagonisten abhängig und nimmt mit steigender Antagonistenkonzentration zu. Das Verhältnis aus EC₅₀-Wert in Anwesenheit eines Antagonisten und EC₅₀-Wert in Abwesenheit eines Antagonisten wird als das Konzentrationsverhältnis (concentration ratio) r bezeichnet:

r={\frac {EC_{50}(+Antagonist)}{EC_{50}(-Antagonist)}}

Das für verschiedene Antagonistenkonzentrationen ermittelte Konzentrationsverhältnis wird als log (r-1) gegen den Logarithmus der molaren Antagonistenkonzentration in einem Diagramm eingetragen. Der Schnittpunkt der Ausgleichsfunktion mit der Abszisse entspricht, bei Vorliegen einer Linearität und einer Steigung der Ausgleichsgeraden von etwa m = 1, dem pA₂-Wert des Antagonisten.

Alternativ dazu ist ein Schild-Plot auf der Basis jedes beliebigen EC_X-Werts theoretisch möglich.

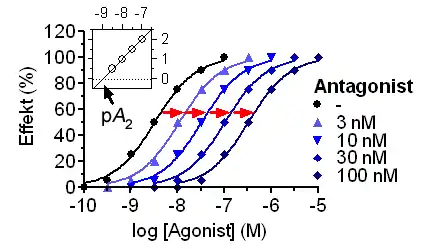
Ermittlung des pA₂-Werts mit Hilfe des Schild-Plots: Steigende Antagonistenkonzentrationen führen zu einer Rechtsverschiebung der Konzentrations-Wirkungskurve und zu einer Abnahme des pEC₅₀-Werts des Agonisten. Aus dieser Rechtsverschiebung lässt sich das Konzentrationsverhältnis r berechnen, das als log (r-1) gegen den Logarithmus der molaren Antagonistenkonzentration im Schild-Plot (eingebettete Abbildung) eingetragen wird und zur Ermittlung des pA₂-Werts dient.

Interpretationen

Außer einer Ermittlung des pA₂-Werts ermöglicht der Schild-Plot auch Aussagen über die qualitative Art des Antagonismus. So ist eine Linearität der Ausgleichsfunktion und eine Steigung der Ausgleichsgeraden von m = 1 ein guter Hinweis auf das Vorliegen eines kompetitiven Antagonismus. Unter diesen Bedingungen entspricht der ermittelte pA₂-Wert der Affinitätskonstanten pK_B des Antagonisten.

Abweichung von der Linearität

Zeigt die Ausgleichsfunktion keinen linearen Verlauf, so kann, auch bei Erfüllung aller anderen Voraussetzungen (insbesondere eine durch den Antagonisten bedingte parallele Rechtsverschiebung der Konzentrations-Wirkungskurve des Agonisten), nicht mehr von einem rein kompetitiven Antagonismus gesprochen werden. Weist die Ausgleichsfunktion zwei oder mehrere lineare Abschnitte auf, so deutet dies auf eine Kompetition zwischen Agonist und Antagonist um zwei oder mehrere Bindungsstellen am Rezeptor.

Abweichung von der Steigung m = 1

Weist bei zumindest annähernder Linearität die Ausgleichsfunktion eine Steigung von m > 1 auf, was in der Praxis eine überproportionale Abnahme der Wirkung des Antagonisten mit abnehmender Konzentration bedeutet, so deutet dies auf eine Inaktivierung oder einen Uptake des Antagonisten unter experimentellen Bedingungen. Dieses Phänomen tritt auch bei nicht ausreichender Inkubationszeit des Antagonisten auf.

Der häufiger zu beobachtende Fall, dass die Ausgleichsgeraden im Schild-Plot eine Steigung von m < 1 aufweist, kann unter anderem auf eine Inaktivierung oder einen Uptake des eingesetzten Agonisten zurückgeführt werden. Auch eine Kompetition von Antagonist und Agonist um verschiedene Bindungsstellen mit verschiedenen Bindungsaffinitäten für diese Liganden kann zu einer Ausgleichsgeraden mit einer Steigung von m < 1 führen.

Alternativen

Alternative Verfahren sind z. B. die Gaddum-Gleichung nach John Gaddum und die Cheng-Prusoff-Gleichung.[2][3][4]

Literatur

O. Arunlakshana, H.O. Schild: Some quantitative uses of drug antagonism. In: Br. J. Pharmacol., 1959, 14, S. 48–58.
T. Kenakin: Pharmacological analysis of drug-receptor interaction. 2. Aufl. Raven Press, New York 1993.

Einzelnachweise

R. R. Neubig, M. Spedding, T. Kenakin, A. Christopoulos: International Union of Pharmacology Committee on Receptor Nomenclature and Drug Classification. International Union of Pharmacology Committee on Receptor Nomenclature and Drug Classification. XXXVIII. Update on terms and symbols in quantitative pharmacology. In: Pharmacol Rev., 2003, Band 55, Nr. 4, S. 597–606. PMID 14657418. PDF.
S. Lazareno, N. J. Birdsall: Estimation of competitive antagonist affinity from functional inhibition curves using the Gaddum, Schild and Cheng-Prusoff equations. In: Br J Pharmacol., 1993, Band 109, Nr. 4, S. 1110–1119. PMID 8401922; PMC 2175764 (freier Volltext).
T. F. Webster: Mixtures of endocrine disruptors: How similar must mechanisms be for concentration addition to apply? In: Toxicology, 2013. PMID 23357612, doi:10.1016/j.tox.2013.01.009.
T. L. Williams, D. A. Smith, N. R. Burton, T. W. Stone: Amino acid pharmacology in neocortical slices: evidence for bimolecular actions from an extension of the Hill and Gaddum-Schild equations. In: Br J Pharmacol., 1988, Band 95, Nr. 3, S. 805–810. PMID 2905185; PMC 1854217 (freier Volltext).

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] R. R. Neubig, M. Spedding, T. Kenakin, A. Christopoulos: International Union of Pharmacology Committee on Receptor Nomenclature and Drug Classification. International Union of Pharmacology Committee on Receptor Nomenclature and Drug Classification. XXXVIII. Update on terms and symbols in quantitative pharmacology. In: Pharmacol Rev., 2003, Band 55, Nr. 4, S. 597–606. PMID 14657418. PDF.

[2] S. Lazareno, N. J. Birdsall: Estimation of competitive antagonist affinity from functional inhibition curves using the Gaddum, Schild and Cheng-Prusoff equations. In: Br J Pharmacol., 1993, Band 109, Nr. 4, S. 1110–1119. PMID 8401922; PMC 2175764 (freier Volltext).

[3] T. F. Webster: Mixtures of endocrine disruptors: How similar must mechanisms be for concentration addition to apply? In: Toxicology, 2013. PMID 23357612, doi:10.1016/j.tox.2013.01.009.

[4] T. L. Williams, D. A. Smith, N. R. Burton, T. W. Stone: Amino acid pharmacology in neocortical slices: evidence for bimolecular actions from an extension of the Hill and Gaddum-Schild equations. In: Br J Pharmacol., 1988, Band 95, Nr. 3, S. 805–810. PMID 2905185; PMC 1854217 (freier Volltext).