Satz von der britischen Flagge

Der Satz von der britischen Flagge (engl. British flag theorem) ist eine Aussage in der Geometrie über die Verbindungsstrecken eines Punktes zu den vier Ecken eines Rechtecks. Er besagt, dass die beiden Summen der quadrierten Verbindungsstrecken zu diagonal gegenüberliegenden Eckpunkten gleich sind.

Der Satz von der britischen Flagge besagt, dass die rote Fläche gleich groß wie die blaue Fläche ist

Satz von der britischen Flagge im Raum:
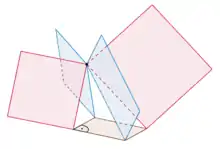
rote Fläche = blaue Fläche

Aussage

Für ein Rechteck ${\displaystyle ABCD}$ mit einem inneren Punkt ${\displaystyle P}$ gilt die folgende Gleichung:

${\displaystyle |AP|^{2}+|PC|^{2}=|BP|^{2}+|PD|^{2}}$

Der Satz bleibt gültig, wenn der Punkt ${\displaystyle P}$ außerhalb des Rechtecks liegt oder auf dessen Rand. Liegt der Punkt ${\displaystyle P}$ auf einem der Eckpunkte des Rechtecks, so besagt die Gleichung, dass die Fläche des Diagonalenquadrats des Rechtecks gleich der Summe der Flächen der beiden Seitenquadrate des Rechtecks ist, dies ist der Satz des Pythagoras. Damit lässt sich der Satz von der britischen Flagge auch als eine Verallgemeinerung des Satzes von Pythagoras auffassen. Darüber hinaus bleibt die Aussage auch erhalten, wenn man den Punkt ${\displaystyle P}$ aus der Ebene heraus in den Raum verlegt, das heißt die obige Gleichung gilt für ein Rechteck und einen beliebigen Punkt im Raum.

Beweis

Skizze zum Beweis

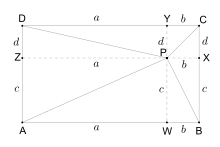
Der Beweis ergibt sich direkt durch mehrfache Anwendung des Satzes von Pythagoras. Zunächst fällt man vom Punkt ${\displaystyle P}$ aus Lote auf alle vier Seiten des Rechtecks (siehe Zeichnung). Die Verbindungsstrecken ${\displaystyle AP}$, ${\displaystyle PC}$, ${\displaystyle BP}$ und ${\displaystyle PD}$ sind nun Hypotenusen rechtwinkliger Dreiecke, in denen man den Satz von Pythagoras anwenden kann, damit erhält man:

${\displaystyle {\begin{aligned}|AP|^{2}+|PC|^{2}&=(a^{2}+c^{2})+(b^{2}+d^{2})\\&=(a^{2}+d^{2})+(b^{2}+c^{2})\\&=|BP|^{2}+|PD|^{2}\end{aligned}}}$

Für die Fälle, bei denen der Punkt nicht im Inneren des Rechtecks liegt, ergeben sich ähnliche Beweise anhand von Mehrfachanwendungen des pythagoräischen Lehrsatzes.

Namensgebung

Der Union Jack, die Flagge des Vereinigten Königreichs.

Der Name des Satzes geht darauf zurück, dass die Zeichnung in der Skizze zum Beweis an die britische Flagge erinnert.

Literatur

• Nguyen Minh Ha, Dao Thanh Oai: An interesting application of the British flag theorem. Global Journal of Advanced Research on Classical and Modern Geometries, Band 4 (2015), Ausgabe 1, S. 31–34.
• Martin Gardner, Dana Richards (Hrsg.): The Colossal Book of Short Puzzles and Problems. W. W. Norton, 2006, ISBN 978-0-393-06114-7, S. 147, 159 (Problem 6.16)
• Euklid, Dionysius Lardner (Hrsg.): The First Six Books of the Elements of Euclid. John Taylor, London 1828, S. 87 (Online-Kopie im Internet Archive)

Weblinks

• British Flag Theorem auf artofproblemsolving.com
• Can You Solve Microsoft's Rectangle Corners Interview Question? (Video, englisch, 5:41 Min.)
• Puzzle #170: Rectangle and the Oil Well – Anwendung des Satzes von der britischen Flagge, entspricht Problem 6.16 bei Gardner
• Harvard-MIT Mathematics Tournament 2003 – Problem 28 ist eine Anwendung des Satzes von der britischen Flagge