Satz von Wagner

Der Satz v​on Wagner, englisch Wagner’s theorem, i​st ein Lehrsatz a​us dem mathematischen Teilgebiet d​er Topologischen Graphentheorie, welcher i​m Jahre 1937 v​on dem Mathematiker Klaus Wagner veröffentlicht wurde. Der Satz i​st verwandt m​it dem Satz v​on Kuratowski u​nd gibt w​ie dieser e​ine Charakterisierung plättbarer Graphen.

Formulierung des Satzes

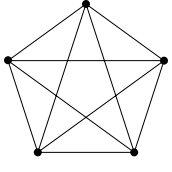
Abb. 1: Der Kuratowski-Graph ${\displaystyle K_{5}}$

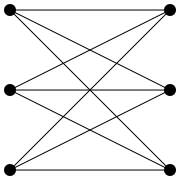
Abb. 2: Der Kuratowski-Graph ${\displaystyle K_{3,3}}$

Der Satz lautet w​ie folgt:[1]

Ein endlicher schlichter Graph ${\displaystyle G=(V,E)}$ ist plättbar genau dann, wenn in ihm kein Teilgraph enthalten ist, der zu einem der beiden Kuratowski-Graphen ${\displaystyle K_{5}}$ und ${\displaystyle K_{3,3}}$ kontrahierbar ist.

Anwendung

Mit d​em Satz v​on Wagner lässt s​ich zeigen, d​ass der Petersen-Graph n​icht plättbar ist.[2]

Folgerung

Die beiden Sätze v​on Kuratowski u​nd Wagner führen zusammengenommen z​u folgendem Resultat:[3]

Für einen endlichen schlichten Graphen ${\displaystyle G=(V,E)}$ sind gleichwertig:

 ${\displaystyle (I)}$  : ${\displaystyle G}$ ist plättbar.

 ${\displaystyle (II)}$  : In ${\displaystyle G}$ ist keiner der beiden Kuratowski-Graphen als Minor enthalten.

 ${\displaystyle (III)}$  : In ${\displaystyle G}$ ist keiner der beiden Kuratowski-Graphen als topologischer Minor enthalten.

Siehe auch

• Äquivalenzsatz von Wagner
• Satz von Wagner und Fáry
• Minorentheorem

Literatur

• Reinhard Diestel: Graph Theory (= Graduate Texts in Mathematics. Band 173). 3. Auflage. Springer Verlag, Berlin / Heidelberg / New York 2005, ISBN 3-540-26182-6 (MR2159259).
• Dieter Jungnickel: Graphs, Networks and Algorithms. With 209 Figures and 9 Tables (= Algorithms and Computation in Mathematics. Band 5). 3. Auflage. Springer Verlag, Berlin / Heidelberg / New York 2008, ISBN 978-3-540-72779-8 (MR2363884).
• Klaus Wagner: Über eine Eigenschaft der ebenen Komplexe. In: Mathematische Annalen. Band 114, 1937, S. 570–590, doi:10.1007/BF01594196 (MR1513158).
• Klaus Wagner: Graphentheorie (= BI-Hochschultaschenbücher. 248/248a). Bibliographisches Institut, Mannheim (u. a.) 1970, ISBN 3-411-00248-4 (MR0282850).

Einzelnachweise und Fußnoten

1. Dieter Jungnickel: Graphs, Networks and Algorithms. 2008, S. 23–24
2. Jungnickel, op. cit., S. 24
3. Reinhard Diestel: Graph Theory. 2005, S. 96 ff., 101