Satz von Viviani

Der Satz von Viviani, benannt nach dem italienischen Mathematiker Vincenzo Viviani (1622–1703), ist eine einfache Aussage über gleichseitige Dreiecke:

Satz von Viviani

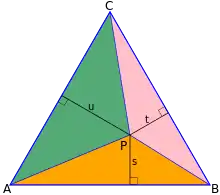
Ist $P$ ein beliebiger Punkt im Inneren eines gleichseitigen Dreiecks, so ist die Summe der Abstände dieses Punktes von den Seiten konstant:

s+t+u=h=3r\,

Dabei bezeichnet $h$ die Höhe des Dreiecks und $r$ den Inkreisradius.

Dies kann man sich geometrisch einfach klarmachen. Die Fläche des gleichseitigen Dreiecks ist so groß wie die Summe der Flächen der farbig markierten Dreiecke.

Für die Fläche des gleichseitigen Dreiecks ABC gilt ${\frac {gh}{2}}$ , wobei $g={\overline {AB}}={\overline {BC}}={\overline {CA}}$ die Grundseite und $h\,$ die Höhe sein soll.

Die Summe der Flächen der farbig markierten Dreiecke ist ${\frac {gs}{2}}+{\frac {gt}{2}}+{\frac {gu}{2}}$ .

Also gilt:

${\frac {gh}{2}}={\frac {gs}{2}}+{\frac {gt}{2}}+{\frac {gu}{2}}$

Damit folgt die Behauptung $h=s+t+u$ .

Der Satz von Viviani lässt sich auf gleichseitige und sogar auf gleichwinklige Polygone verallgemeinern.[1]

Literatur

Heinrich Hermelink: Zur Geschichte des Satzes von der Lotsumme im Dreieck. In: Sudhoffs Archiv für Geschichte der Medizin und der Naturwissenschaften, Bd. 48, H. 3 (September 1964), S. 240–247 (JSTOR 20775106)
Claudi Alsina, Roger B. Nelsen: Charming Proofs: A Journey Into Elegant Mathematics. MAA 2010, ISBN 978-0-88385-348-1, S. 96 (Auszug (Google))
Ken-Ichiroh Kawasaki, Yoshihiro Yagi, Katsuya Yanagawa: On Viviani’s Theorem in Three Dimensions. In: The Mathematical Gazette, Vol. 89, No. 515 (Jul., 2005), S. 283–287 (JSTOR 3621243)
Zhibo Chen, Tian Liang: The Converse of Viviani’s Theorem. In: The College Mathematics Journal, Vol. 37, No. 5 (Nov., 2006), S. 390–391 (JSTOR 27646392)
Elias Abboud: Viviani’s Theorem and Its Extension. In: The College Mathematics Journal, Vol. 41, No. 3 (May 2010), S. 203–211 (JSTOR 10.4169/074683410x488683)
Hans Samelson: Proof without Words: Viviani’s Theorem with Vectors. In: Mathematics Magazine, Vol. 76, No. 3 (Jun., 2003), S. 225 (JSTOR 3219327)

Weblinks

Commons: Viviani's theorem – Sammlung von Bildern, Videos und Audiodateien

Vivianis Theorem auf cut-the-knot (englisch)
Eric W. Weisstein: Viviani’s Theorem. In: MathWorld (englisch).

Einzelnachweise

Michael de Villiers: Crocodiles and Polygons. In: Mathematics in School, Vol. 34, No. 2, Mar. 2005, S. 2–4 (JSTOR 30215779)

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Michael de Villiers: Crocodiles and Polygons. In: Mathematics in School, Vol. 34, No. 2, Mar. 2005, S. 2–4 (JSTOR 30215779)