Satz von Thébault-Yaglom
Der Satz von Thébault-Yaglom (oder auch nur Satz von Thébault) ist eine Aussage der Elementargeometrie und beschreibt eine Eigenschaft von Parallelogrammen. Er besagt, dass die Mittelpunkte der über den Seiten eines Parallelogramms errichteten Quadrate selbst ein Quadrat formen. Benannt ist er nach den Mathematikern Victor Thébault und Isaak Moissejewitsch Jaglom.
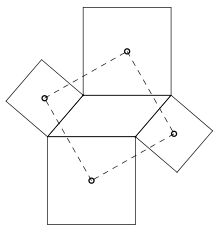
Satz von Thébault
Der Satz lässt sich auf von Parallelogrammen auf beliebige Vierecke verallgemeinern, allerdings bilden die Mittelpunkte der Quadrate dann kein Quadrat mehr, sondern lediglich ein orthodiagonales Viereck mit gleich langen Diagonalen. Diese verallgemeinerte Aussage wird auch als Satz von van Aubel bezeichnet.
Literatur
- Dietmar Herrmann: Die antike Mathematik: Eine Geschichte der griechischen Mathematik, ihrer Probleme und Lösungen. Springer, 2013, S. 420
- I. M. Yaglom: Geometric Transformations, Band 1, Mathematical Association of America, 1962, S. 96f
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.