Satz von Reuschle

Der Satz v​on Reuschle, gefunden u​nd im Jahre 1853 veröffentlicht v​on dem deutschen Gelehrten Karl Gustav Reuschle, i​st ein Lehrsatz d​er elementaren euklidischen Geometrie u​nd als solcher angesiedelt zwischen Dreiecks- u​nd Kreisgeometrie. Er w​ird gelegentlich a​uch als Satz v​on Terquem bezeichnet, n​ach dem französischen Mathematiker Olry Terquem, d​er den Satz bereits 1842 publizierte. Der Satz behandelt e​ine Fragestellung über Schnittpunkteigenschaften gewisser Ecktransversalen, d​ie man i​n ähnlicher Form e​twa im Zusammenhang m​it der Euler-Geraden u​nd dem feuerbachschen Neun-Punkte-Kreis antrifft. Der Beweis v​on Reuschles Lehrsatz beruht a​uf dem Sekantensatz s​owie dem Satz v​on Ceva u​nd dessen Kehrsatz.

Satz von Reuschle

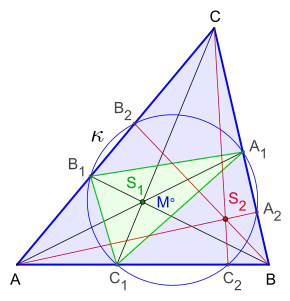
Formulierung des Satzes

Der Satz lässt s​ich in moderner Formulierung angeben w​ie folgt:[1]

Es seien in der euklidischen Ebene ein Dreieck ${\displaystyle ABC}$ gegeben sowie ein Kreis ${\displaystyle {\mathcal {K}}}$ , welcher aus jeder Dreiecksseite eine Kreissehne ausschneiden möge.

Dabei sei für den Eckpunkt ${\displaystyle X\in \{A,B,C\}}$ die in der gegenüberliegenden Dreiecksseite enthaltene Kreissehne die Strecke ${\displaystyle {\overline {{X_{1}}{X_{2}}}}\;(X_{1},X_{2}\in {\mathcal {K}}\;,\;X_{1}\neq X_{2})}$, also ${\displaystyle {\overline {{A_{1}}{A_{2}}}}\subsetneqq {\overline {BC}}\;,\;{\overline {{B_{1}}{B_{2}}}}\subsetneqq {\overline {AC}}\;,\;{\overline {{C_{1}}{C_{2}}}}\subsetneqq {\overline {AB}}}$ .

Jeder Eckpunkt ${\displaystyle X}$ werde mit den beiden gegenüberliegenden Sehnenendpunkten ${\displaystyle X_{1},X_{2}}$ durch die zugehörigen Ecktransversalen ${\displaystyle {XX_{1}},{XX_{2}}}$ verbunden.

Dann gilt:

Treffen sich die ersten drei Ecktransversalen ${\displaystyle {AA_{1}},{BB_{1}},{CC_{1}}}$ in einem gemeinsamen Schnittpunkt ${\displaystyle S_{1}}$, so treffen sich die anderen drei Ecktransversalen ${\displaystyle {AA_{2}},{BB_{2}},{CC_{2}}}$ ebenfalls in einem gemeinsamen Schnittpunkt ${\displaystyle S_{2}}$.

Mit anderen Worten:

Legt man in einem Dreieck ${\displaystyle ABC}$ der euklidischen Ebene durch einen gegebenen inneren Punkt ${\displaystyle S_{1}\in (\operatorname {conv} \{A,B,C\})^{\circ }}$ die drei zugehörigen Ecktransversalen mit den Fußpunkten ${\displaystyle A_{1}\in {\overline {BC}},B_{1}\in {\overline {AC}},C_{1}\in {\overline {AB}}}$ und schneidet der Umkreis des Fußpunktdreiecks ${\displaystyle A_{1}B_{1}C_{1}}$ aus den Dreiecksseiten drei Kreissehnen ${\displaystyle {\overline {{A_{1}}{A_{2}}}}\subsetneqq {\overline {BC}}\;,\;{\overline {{B_{1}}{B_{2}}}}\subsetneqq {\overline {AC}}\;,\;{\overline {{C_{1}}{C_{2}}}}\subsetneqq {\overline {AB}}}$ aus, so haben die so gegebenen Ecktransversalen ${\displaystyle {AA_{2}},{BB_{2}},{CC_{2}}}$ ebenfalls einen gemeinsamen Schnittpunkt ${\displaystyle S_{2}}$ .

Literatur

• Friedrich Joseph Pythagoras Riecke (Hrsg.): Mathematische Unterhaltungen. Erstes Heft. Dr. Martin Sändig, Walluf bei Wiesbaden 1973, ISBN 3-500-26010-1 (Unveränderter Neudruck der Ausgabe Stuttgart 1867–1873).

Weblinks

• Terquem's theorem auf cut-the-knot.org
• Eric W. Weisstein: Cyclocevian Conjugate. In: MathWorld (englisch).

Einzelnachweise

1. Friedrich Joseph Pythagoras Riecke (Hrsg.): Mathematische Unterhaltungen. Erstes Heft. 1973, S. 125