Satz von Harcourt

Der Satz von Harcourt ist eine Aussage in der Elementargeometrie, die eine Beziehung zwischen der Fläche eines Dreiecks und den Abständen seiner Eckpunkte von einer Tangente seines Inkreises beschreibt.

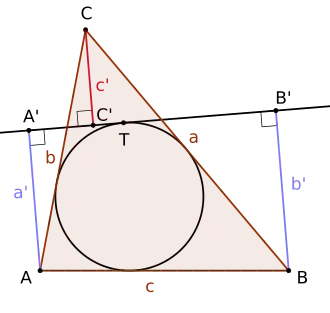
Satz von Harcourt mit positiven (blau) und negativen (rot) Abständen a', b' und c':

2F=aa'+bb'+cc'=a|a'|+b|b'|-c|c'|

Bei einem beliebigen Dreieck ABC mit den Seitenlängen a, b und c seien a' , b' und c' die vorzeichenbehafteten Abstände der Eckpunkte A, B und C von einer Tangente des Inkreises. Dann gilt, dass die Summe der Produkte von vorzeichenbehaftetem Abstand und Seitenlänge dem doppelten Flächeninhalt des Dreiecks entspricht:

2\cdot F=a\cdot a'+b\cdot b'+c\cdot c'

Hierbei besitzt der Abstand ein positives Vorzeichen, wenn er sich auf derselben Seite der Tangente befindet wie der Inkreis, und ein negatives Vorzeichen, wenn er sich auf der anderen Seite der Tangente befindet.

Der Satz ist nach dem irischen Mathematikprofessor J. Harcourt (um 1900) benannt.

Spezialfall

Wenn die Tangente mit der Geraden durch $A$ und $B$ zusammenfällt, so ist mit den obigen Bezeichnungen $a'=b'=0$ und $c'$ ist die Höhe $h_{c}$ . Der Satz von Harcourt lautet in diesem Fall $2\cdot F=c\cdot h_{c}$ bzw. $\textstyle F={\frac {1}{2}}c\cdot h_{c}$ . Das ist die bekannte Formel für den Flächeninhalt eines Dreiecks.

Literatur

Nikolaos Dergiades, Juan Carlos Salazar: Harcourt's Theorem. Forum Geometricorum, Band 3, 2003, S. 117–124.
G. Marie: Exercices de géométrie. 5. Auflage, 1912, S. 750

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.