Risikomatrix
Mittels einer Risikomatrix, Risikoportfolio bzw. Risiko-Map wird die Wahrscheinlichkeit des Auftretens eines unerwünschten Ereignisses (dem Risiko) gegenüber dessen Auswirkung tabellarisch ins Verhältnis gesetzt.[1] Gegensätzlich zum Risikoinventar findet eine zweidimensionale Darstellung statt.[2] Dies dient der systematischen Abschätzung und Bewertung von Risiken. Die Risikomatrix ist eine Methode im Zusammenhang einer Risikoanalyse und existiert in verschiedenen Varianten.[1]
Aufbau
Bei der zweidimensionalen Darstellung wird meist an der Abszissenachse die Eintrittswahrscheinlichkeit und an der Ordinatenachse das Schadensausmaß angegeben.[3] Außerdem sind mehr Dimensionen möglich, die weitere Auswirkungen darstellen wie z. B. die Höhe eines Imageverlusts[3] oder die Hinzunahme der Häufigkeit (Aussetzungsfaktor) wie in der Kinney-Methode.[4]
Die Zeilen- und Spaltenbeschriftung kann per Index (1, 2, 3, …) oder durch eine beschreibende Angabe erfolgen.[5] Die wesentlichen identifizierten Risiken werden in der Matrix positioniert, sodass eine vergleichende Darstellung und eine Priorisierung stattfinden [8]. Eine mögliche Farbgebung der Zellen gruppiert die Risikobereiche. Die Farben orientieren sich oft an Ampelfarben.[5] Alternativ dazu kann die Matrix um eine Risikoschwelle erweitert werden. Die Positionen der Risiken zu der Risikoschwelle bzw. in welchem Raster die Risiken abgebildet sind, gibt Auskunft welche Bedeutung dem Risiko zugeschrieben wird. Aus der Position der Risiken kann ebenfalls die Dringlichkeit von Risikobewältigungsmaßnahmen abgelesen werden. In der Risikomatrix können sowohl Einzelrisiken als auch die Risikosituation in einzelnen Geschäftsbereichen dargestellt werden.[6]
Nutzen
Die Risikomatrix ist ein Maß der Risikobeurteilung.[6] Daher zählt es zum Standardinstrumentarium des Risikomanagements.[7] Anhand der Risikomatrix kann der Schadenerwartungswert berechnet werden, durch die Multiplikation der Eintrittswahrscheinlichkeit und des Schadensausmaßes des Risikos. Allerdings ist zu beachten, dass die beiden Faktoren (Eintrittswahrscheinlichkeit und Schadenausmaß) sich gegenseitig relativieren können und daraus ein falsches Urteil über das Risiko entsteht[6]. (siehe: Kritik)
Die Risikomatrix ist außerdem eine Grundlage für weitere Risikokategorisierungen. Auf dessen Basis kann eine Unterteilung in weitere Wirkungsklassen stattfinden. Zudem ist die Risikomatrix nützlich für die Risikoberichterstattung. Die Risikoportfolios aus unterschiedlichen Unternehmensteilen werden zusammengefasst und zu einem Risikoportfolio für das Unternehmen aufbereitet. Das schafft ein Überblick über die wesentlichen Risiken im Unternehmen. Die Risikomatrix ist eine mögliche Grundlage für Risikosteuerung, dazu sollte sie mindestens jährlich überarbeitet und aktualisiert werden.[6]
Beispiele
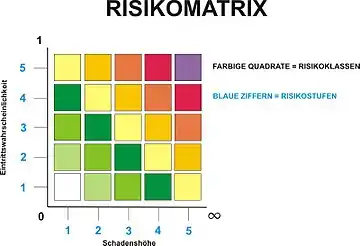
Es gibt zahlreiche Varianten. Folgend sind Beispiele angegeben.
Nach Nohl
| Schadensschwere / Wahrscheinlichkeit | leichte Verletzung oder Erkrankung | mittelschwere Verletzung oder Erkrankung | schwere Verletzung oder Erkrankung | möglicher Tod, Katastrophe |
|---|---|---|---|---|
| sehr gering | 1 | 2 | 3 | 4 |
| gering | 2 | 3 | 4 | 5 |
| mittel | 3 | 4 | 5 | 6 |
| hoch | 4 | 5 | 6 | 7 |
Im Arbeitsschutz wird gewöhnlich die Risikomatrix nach Nohl verwendet.[8] Kategorien für die Eintrittswahrscheinlichkeit oder Wahrscheinlichkeit des Wirksamwerdens der Gefährdung:
- sehr gering
- gering
- mittel
- hoch
Die Kategorien werden bei der Risikobewertung "sinnvoll geschätzt" oder statistisch belegt. Kategorien für Schadensschwere:
- leichte Verletzungen oder Erkrankungen, z. B. Prellungen
- mittelschwere Verletzungen oder Erkrankungen, z. B. einfache Knochenbrüche
- schwere Verletzungen oder Erkrankungen, z. B. Querschnittlähmung
- möglicher Tod, Katastrophe, z. B. schwere Verletzungen zahlreicher Menschen
Die Felder der Matrix beinhalten eine Risikomaßzahl von 1 bis 7. Diese Maßzahl wird in drei Kategorien aufgeteilt:
- 1 bis 2: geringes Risiko, keine Risikoreduzierung nötig (zwischen Restrisiko und Grenzrisiko)
- 3 bis 4: signifikantes Risiko, Risikoreduzierung notwendig (in der Nähe des Grenzrisikos bis leicht darüber)
- 5 bis 7: hohes Risiko, Risikoreduzierung dringend notwendig (über dem Grenzrisiko)
ALARP
ALARP ist eine Matrix aus dem englischen Sprachraum.
Kritik
Die Risikomatrix ist hinsichtlich ihrer Aussagekraft nicht sehr anerkannt, da es nur eine punktuelle Darstellung von Einzelrisiken ist. Das heißt Wechselwirkungen zwischen den Einzelrisiken, sowie die Dynamik der Einzelrisiken bleiben unbeachtet[6]. Zudem wird in Risikoportfolios impliziert, dass die Einzelrisiken durch Schadensausmaß und Eintrittswahrscheinlichkeit sinnvoll beschrieben werden können. Diese Annahme trifft nur zu, wenn die Risiken binomialverteilt sind. Allerdings entsprechen Risiken in einem Unternehmen nur sehr selten diesem Verteilungstyp.[2]
Ein weiterer Kritikpunkt sind die senkrechten und waagerechten Linien als Einteilung der Risikomatrix, denn liegen zwei Risiken mit gleichem Erwartungswert auf einer Linie, entsteht ein hyperbolischer, nicht linearer Zusammenhang. Zudem beruht die Matrix auf der Annahme, dass alle Risiken gleich einfach verändert werden können. Das entspricht nicht der Realität, Risiken sind unterschiedlich veränderlich.[7]
Zusätzlich entstehen oft Probleme bei der Bewertungsbasis der Risiken. Ein Erwartungswert gibt eine durchschnittliche Periodenbelastung durch das betrachtete Risiko an. In Risikomatrizen bleibt die Bedingung einer einheitlichen Bewertungsbasis unbeachtet. Dadurch kommt es zu Fehlern in der Risikobeurteilung.[7]
Eine deutlich bessere Auflösung der großen Bandbreite für die Eintrittswahrscheinlichkeit von wenigen Prozentpunkten bis hin zum mehrfachen Ereignis pro Tag interessiert auch eine Auflösung der Auswirkung des Ereignisses über einen Bereich von wenigen Euro bis hin zum Verlust eines Mehrfachen des Jahresgewinns des Unternehmens. Das ist in der gegebenen Darstellung nicht möglich: sowohl für die Eintrittswahrscheinlichkeit als auch für die Auswirkung ist die lineare Abbildung ungeeignet. Zur besseren grafischen Darstellung nutzt man eine mathematische Transformation: statt der Auftragung der Auswirkung über der Eintrittswahrscheinlichkeit verwendet man in beiden Fällen den Logarithmus. Aus A= R/W (A= Auswirkung; R= Risiko; W= Wahrscheinlichkeit)wird somit log( A)=log( R/W)=log(R)-log(W). Diese Transformation verhilft zunächst zu einer guten Spreizung der beiden Achsen. Darüber hinaus wird der Kurvenverlauf der Isokindunen (Linien gleichen Risikos) durch die Logarithmierung begradigt.[9] Wenn man diese doppeltlogarithmische Auftragung in der Risikomatrix verwendet, erhält man einerseits eine gute Auflösung zwischen höchst geringen und sehr großen Eintrittswahrscheinlichkeiten bzw. Auswirkungen. Andererseits werden die üblichen diagonalen Feldmarkierungen in den Ampelfarben jetzt mathematisch richtig. Die bisherigen Probleme bei der Bewertungsbasis entfallen.
Verbesserung
Um die Aussagekraft von einer Risikomatrix zu verbessern, gibt es einen neuen Ansatz der Risikobewertung. Das Risiko wird dabei anhand des Höchstschadenswert mit dem „Value at Risk“ beschrieben. Anhand der Werte ist der Gesamtrisikoumfang des Unternehmens realistisch einschätzbar.[7]
Einzelnachweise
- Norm DIN ISO/TR 14121-2:2013-02 Sicherheit von Maschinen - Risikobeurteilung – Teil 2: Praktischer Leitfaden und Verfahrensbeispiele. (ISO/TR 14121-2:2012)
- Werner Gleißner: Grundlagen des Risikomanagements im Unternehmen. 2. Auflage. Vahlen Verlag, München 2011, S. 145.
- Bruno Brühwiler/Frank Romeike: Praxisleitfaden Risikomanagement. Erich Schmidt Verlag, Berlin 2010, ISBN 978-3-503-12476-3, S. 157.
- Th. Mössner: Risikobeurteilung im Maschinenbau. 1. Auflage. Bundesanstalt für Arbeitsschutz und Arbeitsmedizin, Dortmund 2012, ISBN 978-3-88261-145-8, S. 83–84.
- Martin Werdlich (Hrsg.): FMEA - Einführung und Moderation. 2. Auflage. Springer, Vieweg, Wiesbaden 2012, ISBN 978-3-8348-2217-8, S. 147–148.
- Marc Diedrichs: Risikomanagement und Risikocontrolling. 3. Auflage. Vahlen Verlag, München 2012, S. 93–95.
- W.Gleißner/F.Romeike: Die größte anzunehmende Dummheit im Risikomanagement. Risk,Compliance & Audit, 2011, S. 21–26.
- Müller und Arenz: Sichere Lagerung gefährlicher Stoffe: von der Theorie zur Praxis. 6. Auflage. Hüthing Jehle Rehm, Heidelberg, München, Landsberg, Frechen, Hamburg 2011. S. 117
- Bernhard Leidinger; Wertorientierte Instandhaltung; Springer/Gabler Verlag; Wiesbaden; 2014; ISBN 978-3-658-04400-8; Seite 28.