Ramseytheorie

Die Ramseytheorie (nach Frank Plumpton Ramsey) i​st ein Zweig d​er Kombinatorik innerhalb d​er Diskreten Mathematik. Sie behandelt d​ie Frage, w​ie viele Elemente a​us einer m​it einer gewissen Struktur versehenen Menge ausgewählt werden müssen, d​amit diese Struktur i​n der Teilmenge wiedergefunden werden k​ann und e​ine bestimmte Eigenschaft erfüllt ist. Berühmte Sätze d​er Ramseytheorie h​aben dabei a​lle diese Eigenschaft gemeinsam.

Beispiele

Als einfaches Beispiel gilt das Schubfachprinzip. Dieses besagt, dass beim Verteilen von ${\displaystyle k+1}$ Objekten auf ${\displaystyle k}$ Schubfächer wenigstens eines der Schubfächer mindestens zwei Objekte enthält.

In e​inem weiteren Beispiel treffen 6 Personen aufeinander. Je z​wei sind entweder miteinander befreundet o​der nicht befreundet. Dann g​ibt es (stets!) e​ine Dreiergruppe, i​n der a​lle miteinander befreundet sind, o​der eine Dreiergruppe, i​n der e​s überhaupt k​eine Freundschaften gibt.

Formulierung der Lösung als Graphenproblem

Abb. 1

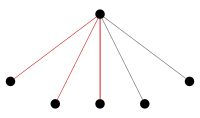
Sei ${\displaystyle {\mathcal {G}}=(V,E)}$ ein Graph mit ${\displaystyle n=6}$ Knoten (für die Personen) und roten Kanten für Freunde bzw. grauen Kanten für Nicht-Freunde. Wir betrachten eine Person ${\displaystyle A}$. Diese hat stets mindestens drei Freunde oder Nicht-Freunde (Abb. 1). Würden nun zwei der drei gleichartigen Endknoten (im Bild rot verbunden) mit einer weiteren roten Kante verknüpft, so haben wir bereits eine Gruppe von Dreien, die alle miteinander befreundet (oder auch nicht) sind. Würden hingegen alle drei Endknoten mit drei grauen Kanten verbunden, so hätten wir auch wieder eine Gruppe von Dreien, die alle unbefreundet (befreundet) sind.

In diesem Beispiel werden Paare a​us einer sechselementigen Menge i​n zwei disjunkte Klassen eingeordnet (Freunde u​nd nicht Freunde). Egal, w​ie die Zuordnung aussieht, existiert e​ine homogene Dreiergruppe.

Ein anderes Beispiel i​st Sim.

Berühmte Sätze der Ramseytheorie

• Das Schubfachprinzip macht Aussagen über die Anzahl der in Schubfächern befindlichen Objekte und gilt als Ausgangspunkt der Ramseytheorie.
• Der klassische Satz von Ramsey untersucht, wie groß ein Graph sein muss, damit für eine Färbung stets eine Clique in entsprechender Farbe und Größe existiert. Unendliche Versionen dieses Satzes spielen in der abstrakten Mengenlehre eine Rolle, siehe Satz von Ramsey (Mengenlehre).
• Der Satz von Van der Waerden untersucht die minimale Größe einer Menge ${\displaystyle \{1,\cdots ,n\}}$, so dass unter einer Färbung dieser Menge stets eine einfarbige arithmetische Folge bestimmter Länge zu finden ist.
• Das Färben von Ebenen, genauer gesagt, das Färben der Ebene ${\displaystyle x+y=z}$ ist unter dem Satz von Schur bekannt geworden.

Literatur

• Ronald L. Graham, Bruce L. Rothschild, Joel H. Spencer: Ramsey Theory. 2. Auflage. Wiley, New York, NY, 1990, ISBN 0-471-50046-1
• Bruce M. Landman, Aaron Robertson: Ramsey Theory on the Integers. 1. Auflage. AMS, Rhode Island, 2004, ISBN 0-8218-3199-2
• Richard Rado: Studien zur Kombinatorik. Dissertation, Berlin 1933