Radargleichung

Mit der Radargleichung (oder Radargrundgleichung) kann die vom Empfänger registrierte Leistung in Abhängigkeit von der Sendeleistung, der Entfernung und den Eigenschaften des reflektierenden Objektes ermittelt werden. Damit kann abgeschätzt werden, ob unter den gegebenen Umständen das Objekt im Empfänger ein ausreichend starkes Signal erzeugt, dass es erkannt werden kann.[1] Aufgrund der unterschiedlichen Reflexionsbedingungen bei Punktzielen (Luftraumaufklärung) und bei Volumenzielen (Wetterradar) werden für diese beiden Fälle unterschiedliche Radargleichungen formuliert. Generell wird die Radargleichung aus dem Abstandsgesetz abgeleitet und gilt wie dieses nur für ungehinderte Abstrahlungen in den freien Raum.

Allgemeiner Überblick

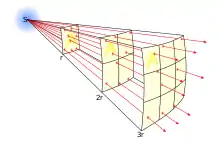
Illustration des Abstandsgesetzes für Energiegrößen

Von wenigen Sonderfällen abgesehen, ist bei Radaranwendungen das Verhältnis von Entfernung zu Wellenlänge so groß, dass die Sendeantenne – unabhängig von ihrer Abmessung – als mathematischer Punkt betrachtet werden kann. Deshalb verteilt sich die Energie wie bei einer Kugelwelle auf immer größere Flächen. Für die Ermittlung der reflektierten Energie muss deshalb unterschieden werden:

Bei einem „Punktziel“ (z. B. ein Flugzeug) ist die Absorptionsfläche konstant; deshalb nimmt die empfangene Energie mit 1/r² ab. Ein Teil davon wird (passiv) zum Radargerät zurückgestrahlt, wobei auch die rückgestrahlte Energie wieder mit 1/r² abnimmt; die Empfangsantenne ist ja ebenfalls ein Punktziel. Insgesamt muss man beide Faktoren multiplizieren und es gilt somit ein 1/r⁴-Zusammenhang.
Bei sehr großen flächigen Zielen wie beispielsweise (nicht zu weit entfernten) Wolken vergrößert sich auch das angestrahlte Volumen mit dem Faktor r². Das heißt, die gesamte, von der Wolke empfangene Energie ist konstant. Ein gewisser Bruchteil davon wird zurückgestrahlt und nur für diesen Rückweg gilt die 1/r²-Abhängigkeit der Energie, so dass auch insgesamt nur ein 1/r²-Zusammenhang gilt.

Interessanterweise gilt diese Vergrößerung nur für ein halbtransparentes Volumen – nicht für eine spiegelnde Fläche. Bei dieser Fläche würde sich die reflektierte Energie über die Zeit verteilen, da die Laufzeit mittig zu dieser Fläche kürzer ist, als bis zum Rand der Fläche. Dieses Problem führt bei Radaraltimetern ebenfalls zu einer wesentlichen zeitlichen Verformung des Echoimpulses auf bis zur Vervielfachung der Dauer des Sendeimpulses.

Mit steigender Entfernung der Wolken füllen diese jedoch einen immer kleineren Anteil der Strahlungskeule aus, denn ein wachsender Teil der gesendeten Energie trifft die Wolke nicht mehr. Dann gilt keiner der beiden vorhergehenden Punkte mehr; es ergibt sich in diesem Fall ein Übergang von einem Abschnitt mit 1/r²- zu einem Abschnitt mit 1/r⁴-Zusammenhang.

Die Radargleichung gilt nur für Primärradar. Ein Sekundärradar nutzt nicht die passive Reflexion von Funkwellen. Es besteht vielmehr aus einer bidirektionalen Funkverbindung. Die Empfangsleistung verringert sich in der Entfernung nach einer 1/r²-Abhängigkeit durch das einfache Abstandsgesetz. Wenn der Transponder antwortet, so ist seine Sendeleistung nicht abhängig von der empfangenen Leistung. Somit gilt für den Rückweg separat eine 1/r²-Abhängigkeit.

Radargleichung für ein Punktziel

Punktziele werden reflektierende Objekte genannt, die das Impulsvolumen eines Radars nicht vollständig ausfüllen, das heißt, dass ihre geometrische Ausdehnung sehr viel kleiner als das Produkt aus Ausbreitungsgeschwindigkeit und Sendeimpulslänge (c₀·τ), sowie sehr viel kleiner als die Breite des Antennendiagramms am Ort der Reflexion sind. Diese Bedingungen liegen zum Beispiel bei Luftraumaufklärungs- und Zielverfolgungsradar vor.

P_r = Empfangsleistung
P_t = Sendeleistung
G_t = Antennengewinn der Sendeantenne
G_r = Antennengewinn der Empfangsantenne
λ = Wellenlänge der Trägerfrequenz
σ = effektive Reflexionsfläche (RCS), σ₀ = kugelförmig streuende Referenzfläche von 1 m²
R_t = Entfernung Sendeantenne – reflektierendes Objekt

R_r = Entfernung reflektierendes Objekt – Empfangsantenne

P_{\text{r}}=P_{\text{t}}{{G_{\text{t}}G_{\text{r}}\lambda ^{2}\sigma } \over {{(4\pi )}^{3}R_{\text{t}}^{2}R_{\text{r}}^{2}}}

Hierbei bedeutet:

Die Gleichung setzt voraus, dass die Entfernung zwischen Objekt und Sender deutlich größer als die Wellenlänge des Radars ist. Das heißt, das Objekt muss sich im Fernfeld des Senders befinden. Weiterhin wird durch das Leistungsverhältnis vorausgesetzt, dass die Dauer des Sendeimpulses etwa der Dauer des Echosignals in der Signalverarbeitung entspricht, dass also kein Pulskompressionsverfahren angewendet wird.

Durch Umstellung der obigen Gleichung nach der Entfernung erhält man eine Form der Radargleichung, die oft in der Praxis verwendet wird, um die betriebliche Leistungsfähigkeit von Radaranlagen zu beurteilen:

R_{\text{max}}={\sqrt[{4}]{\frac {P_{\text{t}}\cdot G^{2}\cdot \lambda ^{2}\cdot \sigma }{P_{{\text{r}}_{\text{min}}}\cdot (4\pi )^{3}\cdot L_{\text{ges}}}}}

Hier wurden der Antennengewinn im Sendefall und Empfangsfall zu G² zusammengefasst: das ist möglich, wenn eine monostatische Radarantenne (R_t ≡ R_r) im Sendemoment das gleiche Antennendiagramm formt, wie während der Empfangszeit (G_t = G_r). Die maximale Reichweite R_max richtet sich dann nach der Empfängerempfindlichkeit P_r,min. Für die praktische Anwendung fließen noch diverse interne und externe Verluste als L_ges mit ein.

Radargleichung für ein Volumenziel

Die Radargleichung für Volumenziele (sprich: für Wetterradar) nutzt radarseitig die gleichen Parameter und Zusammenhänge. Wesentlicher Unterschied sind jedoch die charakteristischen Eigenschaften der Reflexionsfläche, die sich zusätzlich mit zunehmender Entfernung zum Radar ändern. Bei einem Regen ist jeder einzelne Regentropfen sehr viel kleiner als die Wellenlänge des Radargerätes. Deshalb wird die effektive Rückstrahlfläche eines Regentropfens durch die Rayleigh-Streuung bestimmt:

\sigma _{i}={\frac {\pi ^{5}}{\lambda ^{4}}}|K|^{2}D_{i}^{6}

mit:

|K|^{2}=\left|{\frac {\varepsilon -1}{\varepsilon +2}}\right|^{2}

mit D als den Regentropfendurchmesser und ε als dielektrische Konstante. Für die bei Radargeräten üblichen Frequenzbänder L bis X hat Wasser den Faktor |K|²= 0,93 und für Eis gilt |K|²= 0,2.

Bei einem Volumenziel wird das Impulsvolumen nun vollständig durch diese reflektierenden Objekte ausgefüllt. Die Summe dieser reflektierenden Fläche wird mit der temporären Variablen η bezeichnet:

\eta ={\frac {\pi ^{5}}{\lambda ^{4}}}|K|^{2}Z

mit:

Z=\sum _{i=1}^{N}D_{i}^{6}

Das Impulsvolumen V vergrößert sich durch die Divergenz des Antennenstrahls mit der Entfernung zum Radar:

φ = vertikaler Öffnungswinkel des Antennendiagramms
θ = horizontaler Öffnungswinkel
R = Entfernung zum Radar
τ = Sendeimpulsdauer
c₀ = Lichtgeschwindigkeit

V={\frac {\pi \phi \theta R^{2}c_{0}\tau }{8}}

Hierbei bedeuten:

Die internen Parameter des Radars sowie partiell die Freiraumdämpfung werden für meteorologische Belange in einem Faktor C zusammengefasst, der als:

C={\frac {P_{t}\tau G^{2}\theta ^{2}c_{0}\pi ^{3}}{512(2\ln 2)\lambda ^{2}}}

weiterverwendet wird. Hierbei wurde schon berücksichtigt, dass die meisten Wetterradargeräte eine symmetrische Diagrammform mit φ=θ verwenden und deshalb φ·θ=θ² ist. Das führt zu einer stark vereinfachten Form der Radargleichung für Volumenziele, wie sie in der Meteorologie genutzt wird:

P_{r}=\left[{\frac {C}{R^{2}}}\right]\left[|K|^{2}\sum D_{i}^{6}\right]

Mit dieser Gleichung kann nun aus der gemessenen Empfangsleistung direkt auf die Reflektivität geschlossen werden. Diese ist ein Maß für Art und Anzahl der reflektierenden Objekte, wobei dieser Schluss noch nicht eindeutig ist: Viele kleine Wassertröpfchen ergeben die gleiche Reflektivität wie wenige große. Um diese Mehrdeutigkeiten teilweise aufzulösen, wird polarimetrisches Radar genutzt und eine differentielle Reflektivität gemessen.

Literatur

R. J. Doviak, D. S. Zrnic: Doppler Radar and Weather Observations, Academic Press. Second Edition, San Diego Cal. ISBN 978-0-12-221420-2, Seite 562, 1993
J. R. Probert-Jones: The radar equation in meteorology, Quarterly Journal of the Royal Meteorological Society, 1962, Band 88, Ausgabe 378, Seiten 485–495.

Weblinks

Radartutorial (Herleitung der Radargrundgleichung für ein Punktziel)
Radartutorial (Herleitung der Radargleichung für ein Volumenziel)

Einzelnachweise

Radar Handbook Merrill I. Skolnik, 22. Januar 2008, McGraw-Hill-Verlag, ISBN 978-0-07-148547-0, Kapitel 1.4

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[Handbook-1] Radar Handbook Merrill I. Skolnik, 22. Januar 2008, McGraw-Hill-Verlag, ISBN 978-0-07-148547-0, Kapitel 1.4