R-Baum
Ein R-Baum (englisch R-tree) ist eine in Datenbanksystemen verwendete mehrdimensionale (räumliche) dynamische Indexstruktur. Ähnlich wie bei einem B-Baum handelt es sich hier um eine balancierte Indexstruktur.
Verwendungszweck
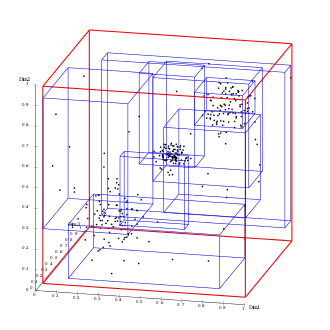
Ein R-Baum erlaubt die schnelle Suche in mehrdimensionalen ausgedehnten Objekten. Neben einfachen Punkten gehören dazu auch Polygone im zweidimensionalen Raum und geometrische Körper im dreidimensionalen Raum. Typisch sind aber auch hochdimensionale Objekte, wie sie in der Mathematik oder Bioinformatik vorkommen. Hochdimensional bedeutet hierbei, dass die Anzahl der unabhängigen Suchkriterien in der Größenordnung von 100–1.000.000 liegt. Erfahrungswerte sagen aber, dass ein R-Baum nur bis etwa 10 Dimensionen gut funktioniert. Dies ist aber von den konkreten Daten abhängig, und es gibt R-Baum-Varianten, die hier Optimierungen enthalten.
Ein R-Baum kann effizient Bereichs-Anfragen (d. h. Rechtecks- bzw. Intervall-Anfragen) beantworten. Auch die Auswertung von nächste-Nachbar-Anfragen ist effizient möglich für geometrische Distanzen, die mit Rechtecken begrenzt werden können. Ein R-Baum ist dynamisch, d. h., er kann bei Änderungen effizient aktualisiert werden.
Typisches Einsatzgebiet eines R-Baum-Index sind Geodatenbanken. Hier werden z. B. Straßendaten, Grenzbereiche oder Gebäudedaten verwaltet. Diese werden als Polygone in der Datenbank gespeichert. Der R-Baum erlaubt später das effiziente Auffinden bestimmter Polygone anhand der Ortskoordinaten. Da hier Rechtecks-Anfragen (z. B. Kartenausschnitte) typisch sind, ist ein R-Baum dazu gut geeignet.
Weniger Vorteile bringt der R-Baum bei Unterraum-Anfragen (Anfragen, bei denen nicht alle Dimensionen spezifiziert sind – hier entstehen sehr große Anfragebereiche) oder bei nicht-geometrischen Distanzen (die nicht in Rechtecksbereiche übersetzt werden können). Hier sind andere Indexstrukturen besser geeignet.
Realisierung
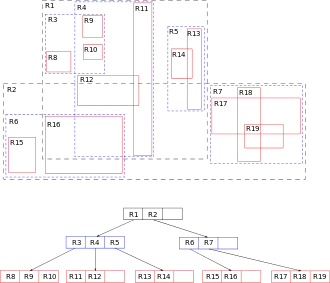
Das Prinzip eines R-Baums als räumliche Indexstruktur wurde von Antonin Guttman vorgestellt.[1] Ähnlich wie bei einem B+-Baum enthalten Blattknoten eines R-Baumes die zu indizierenden räumlichen Daten. Im Gegensatz zu diesem enthält er aber keine trennenden Schlüssel, sondern speichert in den Indexknoten rechteckige Datenregionen (minimal umgebende Rechtecke), die alle im Teilbaum darunter liegenden Datenregionen umfassen. In den Datenseiten können Datenpunkte, rechteckige Bereiche oder auch Polygone gespeichert sein. Letztere werden oft aber durch ein minimal umgebendes Rechteck approximiert.
Realisiert wird die Speicherung eines Rechtecks durch die Angabe von Intervallen für alle seine Dimensionen. Mithilfe eines R-Baumes können Punkt- oder Enthaltenseinanfragen wie „ist Punkt P in Figur F enthalten?“, „ist Figur F1 in Figur F2 enthalten?“ oder „welche Figuren sind in Figur F enthalten?“ beantwortet werden. Durch die verwendete Näherung (minimal umgebende Rechtecke) in den Blattknoten kann es zu Fehltreffern kommen, die durch Überprüfung der Anfrage an den konkreten Objekten aufgelöst werden müssen. Bei Polygonen spricht man bei der Berechnung auf den Rechtecken von einem „Filterschritt“, bei dem Test mit dem exakten Polygon von dem „Verfeinerungsschritt“. Die eigentliche Indexstruktur liefert hier also nur Kandidaten.
Varianten
R*-Baum
Eine beliebte R-Baum-Variation ist der R*-Baum von Norbert Beckmann, Hans-Peter Kriegel, Ralf Schneider und Bernhard Seeger.[2] Diese Variante versucht, durch eine weiterentwickelte Split-Strategie das Überlappen von Rechtecksregionen zu minimieren. Dadurch brauchen bei einer Suchanfrage meistens weniger Teilbäume durchsucht zu werden, und die Anfragen an den Baum werden dadurch effizienter. Zusätzlich können beim Überlauf einer Seite auch Elemente neu in den Baum eingefügt werden (re-insert), was eine Aufteilung (engl. "split") (und die damit unter Umständen steigende Höhe des Baumes) vermeiden kann. Dadurch wird ein höherer Füllgrad erreicht und dadurch ebenfalls eine verbesserte Effizienz. Der resultierende Baum ist aber stets auch ein R-Baum, die Anfragestrategie ist unverändert.
R+-Baum
Im R-Baum und R*-Baum konnten sich die Suchräume überlappen. Das ist im R+-Baum nicht erlaubt (die Suchräume sind hier disjunkt). Umschließende Rechtecke werden falls notwendig an den Suchraumgrenzen „abgetrennt“. Hierbei können auch Objekte „zerschnitten“ werden, so dass ein Teil des Objekts sich im einen Suchraum und ein anderer Teil des Objekts sich im anderen Suchraum befindet. In solchen Fällen müssen Objekte dann mehrfach im Baum abgelegt werden. R+-Bäume lassen sich für statische Daten gut vorberechnen (insbesondere für Punktdaten, bei denen ein solches Zerschneiden entfällt). Bei Änderungen wird es jedoch aufwendiger, die Disjunktheit sicherzustellen.
Probleme von R-Bäumen
Wie jede Indexstruktur stellen R-Bäume einen Kompromiss dar. Die Verwaltung und Aktualisierung des Baumes erfordert zusätzliche Berechnungen, es wird auch zusätzlicher Speicher für die Indexseiten benötigt. Umgekehrt kann dafür der Baum (bei geeigneten Anfragen und Daten) oftmals die gesuchten Datensätze schneller auffinden. Nimmt man erhöhten Speicherverbrauch und erhöhte Rechenzeit bei Änderungen in Kauf, so kann man oft bessere Leistung bei Suchanfragen erzielen. So wird ein R+-Baum meist mehr Speicher benötigen als ein R- oder R*-Baum. Er liefert höhere Leistung bei der Suche, dafür benötigt er mehr Aufwand bei Änderungen.
R*-Bäume sind eine beliebte Wahl, da sie ohne zusätzlichen Speicheraufwand (gegenüber einem R-Baum; im Gegensatz zum R+-Baum der Objekte bei Bedarf mehrfach speichert) auskommen, und ihr Implementierungs- und Rechenaufwand nicht wesentlich höher ist als bei einem R-Baum. Genauer gesagt ist ein R-Baum im Speicher auch stets ein R*-Baum, sie unterscheiden sich nur bei der Einfüge- und Split-Strategie.
R-Bäume sind reihenfolgeabhängig, eine wichtige Maßnahme zur Optimierung sind daher „bulk loads“, bei denen der Baum nicht durch elementweises Einfügen aufgebaut wird, sondern versucht wird, direkt einen verbesserten Baum zu konstruieren. Hierzu werden oft die Elemente zunächst sortiert und dann der Baum bottom-up konstruiert. Wird ein R-Baum elementweise in einer ungünstigen Reihenfolge gefüllt, so kann er eine (geometrisch) unbalancierte Struktur aufweisen. Ein optimierter R-Baum hat zwar die annähernd gleiche Tiefe, seine Regionen überlappen sich aber weniger und überdecken den Datenraum daher gleichmäßiger.
In höheren Dimensionen tritt der sogenannte Fluch der Dimensionalität auf. Beim R-Baum führt das dazu, dass sich die entstehenden Rechtecksregionen zu immer größeren Teilen überlappen, wodurch die Suche immer größere Teile des Baumes verarbeiten muss. Dies reduziert die Leistung der Indexstruktur. Der X-Baum von Stefan Berchtold, Daniel A. Keim und Hans-Peter Kriegel[3] stellt hier eine wichtige Variation des R-Baum-Konzeptes für höhere Dimensionalitäten dar. Eine wichtige Maßnahme hierbei sind sogenannte „Supernodes“, das sind vergrößerte Seiten, die vom X-Baum verwendet werden, um ungünstige Splits (mit einer hohen Überlappung) zu vermeiden. Im Extremfall kann er so auch zu einer linearen Datei degenerieren, was gewünscht sein kann.
Während ein R-Baum als dynamische Indexstruktur konzipiert ist, so kann sich seine Leistung durch systematische Einfüge- oder Löschoperationen verschlechtern. In solchen Fällen kann es sinnvoll sein, den Baum von Zeit zu Zeit durch einen bulk load neu aufzubauen, um ihn zu optimieren. Es gibt auch inkrementelle Optimierungsstrategien (wie die re-inserts im R*-Baum), mit denen ein Datenbanksystem in Leerlaufzeiten den Index verbessern kann.
Verfügbarkeit
Eine Referenzimplementierung des R*-Baums ist im Software-Paket ELKI des Lehrstuhls von Professor Hans-Peter Kriegel verfügbar, inklusive Implementierungen eines M-Baumes und anderen Vergleichsverfahren.
Ein R*-Baum findet sich auch beispielsweise in den Datenbanksystemen SQLite (für 2–5 Dimensionen) und Oracle (für 2–4 Dimensionen).
Bei PostgreSQL war der Indextyp „rtree“ bis Version 8.1 vorhanden[4], wurde dann jedoch von der Generalized-Search-Tree-Schnittstelle (GiST) abgelöst, da er keine nennenswerten Vorteile besaß.[5]
Siehe auch
- Quadtree, K-d-Baum, UB-Baum, Bereichsbaum, Gridfile als Alternative
Weblinks
- Splitting Rules (englisch)
- R-Tree Demonstration (Java-Applet)
Einzelnachweise
- A. Guttman: R-Trees: A Dynamic Index Structure for Spatial Searching. In: Proc. ACM SIGMOD International Conference on Management of Data. 1984, doi:10.1145/602259.602266 (PDF).
- N. Beckmann, Hans-Peter Kriegel, R. Schneider, B. Seeger: The R*-Tree: An Efficient and Robust Access Method for Points and Rectangles. In: Proc. 1990 ACM SIGMOD International Conference on Management of Data. 1990, S. 322–331, doi:10.1145/93597.98741 (PDF).
- S. Berchtold, D. A. Keim, Hans-Peter Kriegel: The X-Tree: An Index Structure for High-Dimensional Data. In: VLDB Conference. 1996, S. 28–39 (PS).
- CREATE INDEX. 1. Januar 2012, abgerufen am 7. Februar 2021 (englisch).
- CREATE INDEX. 12. November 2020, abgerufen am 7. Februar 2021 (englisch).