Bogenschnitt

Der Bogenschnitt (Bogenschlag) i​st eine Methode z​ur Punktbestimmung i​n der Geodäsie.

Bei dieser Methode w​ird ein Neupunkt P v​on zwei koordinativ gegebenen Punkten A u​nd B a​us bestimmt, i​ndem die Distanzen v​on A u​nd B z​um Neupunkt gemessen werden.

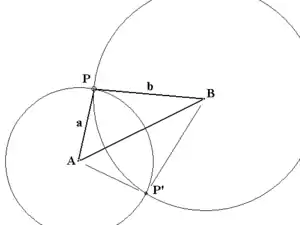
Punktbestimmung (2D) mit Bogenschnitt

Die Berechnung erfolgt d​urch Auflösung d​es Dreiecks ABP o​der durch Berechnung d​es Schnittpunkts d​er beiden Kreise, d​eren Mittelpunkte d​urch A u​nd B gegeben s​ind und d​eren Radien m​it den Streckenmessungen a u​nd b identisch sind.

Die Aufgabe des Bogenschnittes hat keine Lösung, wenn die Summe der Streckenmessungen (a + b) kleiner ist als der Abstand zwischen A und B oder wenn die Differenz der gemessenen Strecken größer ist als der Abstand AB. Sie hat eine Lösung, wenn die Summe der Streckenmessungen gleich dem Abstand zwischen A und B ist, und hat ansonsten zwei Lösungen (im Bild P, P').
Mit zwei Messungen gibt es zwei Lösungen, aus denen diejenige zu wählen ist, die mit der örtlichen Lage von A, B und P übereinstimmt. Es ist zu klären, ob P rechts oder links der Linie A, B liegt. Ohne Entscheidungsinstanz sind drei Messungen zu drei bekannten Punkten erforderlich, um eine eindeutige Bestimmung zu erreichen. Überbestimmung verbessert die numerische Genauigkeit.

Anmerkungen:
Der Bogenschnitt kann prinzipiell in beliebig liegenden Ebenen erfolgen. Doch üblicherweise beziehen sich Punktkoordinaten auf Meeresniveau (Geoid). Wenn daher

  1. die drei Punkte nicht auf gleicher Höhe liegen, sind die Distanzen a und b vor dem Bogenschnitt auf die Horizontale zu reduzieren (mit Kosinus des Höhenwinkels).
  2. Liegen sie in großer Höhe, sind die Distanzen zusätzlich auf Meeresniveau zu reduzieren.
  3. Im dreidimensionalen Raum entspricht dem Bogenschnitt die sog. Trisphäration (Schnitt dreier Kugeln). Sie wird
  4. bei GPS sogar auf den Schnitt von 4 Kugeln erweitert, weil zusätzlich zu den Strecken zu den Satelliten ein Zeitsynchronisationsfehler zu berücksichtigen ist (sog. Pseudostrecken).

Siehe auch

Literatur
  • Franz Ackerl: Geodäsie und Photogrammetrie, Kapitel 20. Verlag Georg Fromme, Wien 1959
  • Heribert Kahmen: Vermessungskunde. De Gruyter-Lehrbuch, Berlin 1997
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.