Projektionssatz (Dreieck)

Der Projektionssatz i​st eine Aussage a​us der Elementargeometrie, d​ie eine Verallgemeinerung d​es Kathetensatzes a​uf beliebige Dreiecke darstellt:

Für zwei Seiten in einem beliebigen Dreieck sind diejenigen Rechtecke flächeninhaltsgleich die aus einer Seite und der orthogonalen Projektion der anderen auf sie gebildet werden.

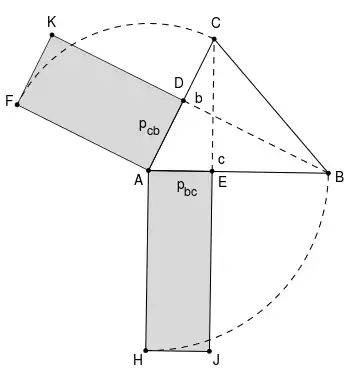
Flächengleichheit der beiden grauen Rechtecke:
mit ${\displaystyle c=AB,\,b=AC}$
und ${\displaystyle p_{bc}=AE,\,p_{cb}=AD}$
gilt ${\displaystyle |c|\cdot |p_{bc}|=|b|\cdot |p_{cb}|}$

In einem beliebigen Dreieck ${\displaystyle \triangle ABC}$ mit Seiten a, b und c bezeichne p_xy die Projektion der Seite x auf die Seite y, dann gilt:

${\displaystyle {\begin{aligned}|c|\cdot |p_{bc}|&=|b|\cdot |p_{cb}|\\|a|\cdot |p_{ba}|&=|b|\cdot |p_{ab}|\\|c|\cdot |p_{ac}|&=|a|\cdot |p_{ca}|\\\end{aligned}}}$

In einem rechtwinkligen Dreieck ${\displaystyle \triangle ABC}$ mit einem rechten Winkel in C entsprechen die Projektionen p_cb und p_ca den Seiten b und a. Damit liefert der Projektionssatz dann:

${\displaystyle {\begin{aligned}|c|\cdot |p_{bc}|&=|b|^{2}\\|c|\cdot |p_{ac}|&=|a|^{2}\end{aligned}}}$

Man erhält a​lso den Kathetensatz d​es Euklid.

Literatur

• Hans Schupp: Elementargeometrie (Uni-Taschenbücher 669 Mathematik). Schöningh, Paderborn 1977, ISBN 3-506-99189-2, S. 117–118