Planetenrollengewindetrieb

Planetenrollengewindetriebe[1] sind Gewindetriebe in der Antriebstechnik, bei denen geschliffene Planetengewinderollen, in eine Umlaufmutter zwischen zwei Lochkränzen gefasst, um eine spezielle Rollengewindespindel rotieren, wodurch sich eine axiale Relativbewegung zwischen Mutter und Spindel ergibt. In der typischen Anwendung, z. B. beim Verfahren des Schlittens einer Werkzeugmaschine, rotiert die Gewindespindel, während die Mutter in Umfangsrichtung feststeht und linear verschoben wird. Dieses System gibt es ebenfalls als invertierte Version, bei der sich Planetengewinderollen und Lochkränze axial gemeinsam mit der Schubstange bewegen. Diese Bauart lässt sich mit einem Hohlwellenmotor zu einem kompakten Aktuator mit glatter Schubstange kombinieren, der in seiner äußeren Erscheinung einem Pneumatikzylinder ähnelt.

Planeten­rollen­gewinde­trieb

Funktionsweise
Detailanimation

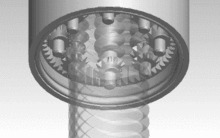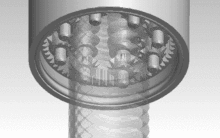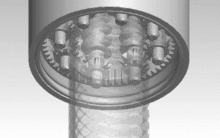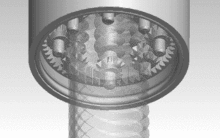
Der Name Planetenrollengewindetrieb leitet sich von der Art der Rotation der Rollen um die Spindel ab, die wie Planeten um ein Zentralgestirn kreisen. Dabei werden Spindel-, Rollen- und Mutterdurchmesser so gewählt, dass die Umfangsgeschwindigkeiten von Spindel und Rollen übereinstimmen. Die Synchronisation übernimmt ein in die Mutter integrierter Ring mit einer Innenverzahnung, der in Ritzel an den Enden der Rollen eingreift. Da sich die Wälzkörper im Unterschied zu den Kugeln im Kugelgewindetrieb oder dem Rollengewindetrieb mit Rollenrückführung in Längsrichtung nicht relativ zur Mutter bewegen, ist kein Rückführmechanismus notwendig. Dies ermöglicht höhere Drehzahlen als beispielsweise bei Kugelumlaufspindeln.

Die h​ohen Tragzahlen d​er Rollengewindetriebe ergeben s​ich aus d​er großen Anzahl tragender Kontaktflächen. Ein typischer Rollengewindetrieb h​at rund 10 Rollen m​it 15 b​is 25 Windungen. Somit ergeben s​ich 100–200 Kontaktpunkte. Um m​it einem Kugelgewindetrieb d​ie gleiche Tragzahl z​u erreichen, wären entweder e​ine große Anzahl o​der sehr große Kugeln notwendig. Eine Gewinderolle erfüllt s​omit die Funktion e​iner großen Zahl v​on übereinander liegenden Kugeln a​uf deutlich geringerem Raum.

Mit Rollengewindetrieben lassen s​ich sehr kleine Gewindesteigungen realisieren. Bei Kugelgewindetrieben m​uss die Steigung größer a​ls der Kugeldurchmesser sein, d​amit sich d​eren Laufbahnen n​icht überschneiden. Beim Rollengewindetrieb entfällt d​iese Einschränkung. Allerdings n​immt bei großen Steigungen d​er Gleitanteil b​ei der Rollenbewegung zu, wodurch d​er Wirkungsgrad sinkt.

Daher s​ind diese lineartechnischen Antriebe insbesondere für h​ohe Lasten u​nd mittlere Geschwindigkeiten geeignet.

Lebensdauer

Die Berechnung der Lebensdauer () eines Rollengewindetriebs erfolgt wie bei Wälzlagern und Kugelgewindetrieben über die dynamische Tragzahl . Da ohnehin nur Axialkräfte () zulässig sind, entfallen Radial- und Axialbeiwert. Für die charakteristische Ermüdungslebensdauer des Planetenrollengewindetriebs gilt:

Wie bei Wälzlagern handelt es sich hierbei um die Lebensdauer, die mit einer Wahrscheinlichkeit von 90 % erreicht oder übertroffen wird. Die Lebensdauer von Planetenrollengewindetrieben ist typischerweise höher als die von Kugelgewindetrieben.

Anwendungen

Insbesondere in Kombination mit Servomotoren und der entsprechenden Regelungstechnik ergeben sich vielfältige Anwendungsmöglichkeiten. Grundsätzlich ist zum Beispiel ein Ersatz von Hydraulik- und Pneumatikzylindern möglich. Hierbei kann aufgrund des besseren Wirkungsgrads oftmals eine Energieeinsparung erzielt werden. Im Vergleich zur Hydraulik entfällt auch die Hydraulikflüssigkeit und die damit verbundenen Umwelt- und Sicherheitsprobleme. Auch die Positions- und Geschwindigkeitsregelung ist aufgrund der hohen Steifigkeit des Gesamtsystems in der Regel deutlich einfacher als bei hydraulischen oder pneumatischen Antriebssystemen. Typische Anwendungen sind Bewegungssimulatoren, Pressen, Roboterschweißzangen, Dosieranlagen, Montagestände und Ventilantriebe. Dabei werden üblicherweise Kräfte bis ca. 200–300 kN und Geschwindigkeiten bis etwa 1,5 m/s benötigt.

Siehe auch

Einzelnachweise
  1. Manfred Weck: Werkzeugmaschinen 2 - Konstruktion und Berechnung. Springer DE, 2006, ISBN 978-3-540-30438-8, S. 479
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.