Plücker-Matrix

Die Plücker-Matrix ist eine spezielle schiefsymmetrische ${\displaystyle 4\times 4}$-Matrix, die eine Gerade im projektiven Raum charakterisiert. Die Matrix ist durch die 6 Plücker-Koordinaten mit 4 Freiheitsgraden beschrieben. Benannt sind sie nach dem deutschen Mathematiker Julius Plücker.

Definition

Eine Gerade im Raum ist definiert durch zwei verschiedene Punkte ${\displaystyle A=\left(A_{0},A_{1},A_{2},A_{3}\right)^{\top }\in \mathbb {R} {\mathcal {P}}^{3}}$ und ${\displaystyle B=\left(B_{0},B_{1},B_{2},B_{3}\right)^{\top }\in \mathbb {R} {\mathcal {P}}^{3}}$ in homogenen Koordinaten des projektiven Raums. Ihre Plücker-Matrix ist:

${\displaystyle [\mathbf {L} ]_{\times }\propto \mathbf {A} \mathbf {B} ^{\top }-\mathbf {B} \mathbf {A} ^{\top }=\left({\begin{array}{cccc}0&-L_{01}&-L_{02}&-L_{03}\\L_{01}&0&-L_{12}&-L_{13}\\L_{02}&L_{12}&0&-L_{23}\\L_{03}&L_{13}&L_{23}&0\end{array}}\right)}$

Wobei die schiefsymmetrische ${\displaystyle 4\times 4}$-Matrix durch die 6 Plücker-Koordinaten

${\displaystyle \mathbf {L} \propto (L_{01},L_{02},L_{03},L_{12},L_{13},L_{23})^{\top }}$

mit

${\displaystyle L_{ij}=A_{i}B_{j}-B_{i}A_{j}}$

beschrieben ist. Die Plücker-Koordinaten erfüllen d​ie Graßmann-Plücker-Relation

${\displaystyle L_{01}L_{23}-L_{02}L_{13}+L_{03}L_{12}=0}$

und sind bis auf skalare Vielfache definiert. Jede Plücker-Matrix besitzt lediglich Rang 2 und vier Freiheitsgrade (wie jede Gerade in ${\displaystyle \mathbb {R} ^{3}}$). Sie ist unabhängig von der Wahl der Punkte A und B und ist außerdem eine Verallgemeinerung der Geradengleichung bzw. des Kreuzprodukts für sowohl den Schnitt zweier Geraden, als auch der Verbindungsgeraden durch zwei Punkte in der projektiven Ebene.

Eigenschaften

Die Plücker-Matrix erlaubt e​s folgende geometrische Operationen i​m Matrix-Vektor-Produkt auszudrücken:

• Ebene enthält Gerade: ${\displaystyle \mathbf {0} =[\mathbf {L} ]_{\times }\mathbf {E} }$

• ${\displaystyle \mathbf {X} =[\mathbf {L} ]_{\times }\mathbf {E} }$ ist der Schnittpunkt der Geraden ${\displaystyle \mathbf {L} }$ mit der Ebene ${\displaystyle \mathbf {E} }$ ('Meet')

• Punkt liegt auf Gerade: ${\displaystyle \mathbf {0} =[{\tilde {\mathbf {L} }}]_{\times }\mathbf {X} }$

• ${\displaystyle \mathbf {E} =[{\tilde {\mathbf {L} }}]_{\times }\mathbf {X} }$ ist die gemeinsame Ebene ${\displaystyle \mathbf {E} }$, die den Punkt ${\displaystyle \mathbf {X} }$ und die Gerade ${\displaystyle \mathbf {L} }$ enthält ('Join').

• Richtung einer Geraden: ${\displaystyle [\mathbf {L} ]_{\times }\pi ^{\infty }=[\mathbf {L} ]_{\times }(0,0,0,1)^{\top }=(-L_{03},-L_{13},-L_{23},0)^{\top }}$ (Anmerkung: Kann auch als Ebene durch den Koordinatenursprung, orthogonal zur Geraden interpretiert werden)

• Punkt der am dichtesten am Koordinatenursprung liegt: ${\displaystyle \mathbf {X} _{0}\cong [\mathbf {L} ]_{\times }[\mathbf {L} ]_{\times }\pi ^{\infty }.}$

Eindeutigkeit

Zwei beliebige unterschiedliche Punkte auf der Geraden lassen sich durch Linearkombination von ${\displaystyle \mathbf {A} }$ und ${\displaystyle \mathbf {B} }$ finden:

${\displaystyle \mathbf {A} ^{\prime }\propto \mathbf {A} \alpha +\mathbf {B} \beta {\text{ und }}\mathbf {B} ^{\prime }\propto \mathbf {A} \gamma +\mathbf {B} \delta }$.

Ihre Plücker-Matrix i​st dann:

${\displaystyle [\mathbf {L} ^{\prime }]_{\times }=\mathbf {A} ^{\prime }\mathbf {B} ^{\prime \top }-\mathbf {B} ^{\prime }\mathbf {A} ^{\prime \top }=(\mathbf {A} \alpha +\mathbf {B} \beta )(\mathbf {A} \gamma +\mathbf {B} \delta )^{\top }-(\mathbf {A} \gamma +\mathbf {B} \delta )(\mathbf {A} \alpha +\mathbf {B} \beta )^{\top }={\underset {\lambda }{\underbrace {(\alpha \delta -\beta \gamma )} }}[\mathbf {L} ]_{\times },}$

also bis auf ein skalares Vielfaches identisch zu ${\displaystyle [\mathbf {L} ]_{\times }}$.

Schnittpunkt mit Ebene

Der Schnittpunkt einer Geraden im Raum L mit einer Ebene E als Multiplikation mit der Plücker-Matrix

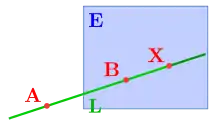
Es sei ${\displaystyle \mathbf {E} =(E_{0},E_{1},E_{2},E_{3})^{\top }\in \mathbb {R} {\mathcal {P}}^{3}}$ eine Ebene mit der Gleichung

${\displaystyle E_{0}x+E_{1}y+E_{2}z+E_{3}=0.}$

die die Gerade ${\displaystyle \mathbf {L} }$ nicht enthält. Dann beschreibt das Matrix-Vektor-Produkt der Plückermatrix mit der Ebene einen Punkt

${\displaystyle \mathbf {X} =[\mathbf {L} ]_{\times }\mathbf {E} =\mathbf {A} {\underset {\alpha }{\underbrace {\mathbf {B} ^{\top }\mathbf {E} } }}-\mathbf {B} {\underset {\beta }{\underbrace {\mathbf {A} ^{\top }\mathbf {E} } }}=\mathbf {A} \alpha +\mathbf {B} \beta ,}$

der auf der Geraden ${\displaystyle \mathbf {L} }$ liegt, da er eine Linearkombination von ${\displaystyle \mathbf {A} }$ und ${\displaystyle \mathbf {B} }$ ist. ${\displaystyle \mathbf {X} }$ liegt auch auf der Ebene ${\displaystyle \mathbf {E} }$

${\displaystyle \mathbf {E} ^{\top }\mathbf {X} =\mathbf {E} ^{\top }[\mathbf {L} ]_{\times }\mathbf {E} ={\underset {\alpha }{\underbrace {\mathbf {E} ^{\top }\mathbf {A} } }}{\underset {\beta }{\underbrace {\mathbf {B} ^{\top }\mathbf {E} } }}-{\underset {\beta }{\underbrace {\mathbf {E} ^{\top }\mathbf {B} } }}{\underset {\alpha }{\underbrace {\mathbf {A} ^{\top }\mathbf {E} } }}=0,}$

und m​uss daher d​er Schnittpunkt d​er Gerade u​nd der Ebene sein.

Des Weiteren gilt, dass das Produkt der Plücker-Matrix mit einer Ebene genau dann den Nullvektor ergibt, wenn die Gerade ${\displaystyle \mathbf {L} }$ in der Ebene enthalten ist:

${\displaystyle \alpha =\beta =0\iff \mathbf {E} }$ enthält ${\displaystyle \mathbf {L} .}$

Duale Plücker-Matrix

Die gemeinsame Ebene G eines Punktes X mit einer Geraden im Raum L als Multiplikation mit der dualen Plücker-Matrix

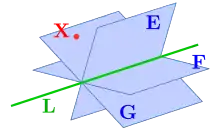
Im realen projektiven Raum h​aben Punkte u​nd Ebenen d​ie gleiche Darstellung a​ls homogene 4-Vektoren u​nd die algebraische Beschreibung i​hrer Beziehung (Punkt l​iegt auf Ebene) i​st symmetrisch. Durch Vertauschen d​er Bedeutung v​on Punkten u​nd Ebenen e​iner Aussage erhält m​an daher e​ine duale Aussage, d​ie ebenfalls w​ahr ist.

Im Fall d​er Plücker-Matrix, existiert d​ie duale Darstellung e​iner Geraden i​m Raum a​ls Schnitt zweier Ebenen

${\displaystyle E=\left(E_{0},E_{1},E_{2},E_{3}\right)^{\top }\in \mathbb {R} {\mathcal {P}}^{3}}$

und

${\displaystyle F=\left(F_{0},F_{1},F_{2},F_{3}\right)^{\top }\in \mathbb {R} {\mathcal {P}}^{3}}$

in homogenen Koordinaten d​es projektiven Raums. Ihre Plücker-Matrix ist:

${\displaystyle [{\tilde {\mathbf {L} }}]_{\times }=\mathbf {E} \mathbf {F} ^{\top }-\mathbf {F} \mathbf {E} ^{\top }}$

und

${\displaystyle \mathbf {G} =[{\tilde {\mathbf {L} }}]_{\times }\mathbf {X} }$

beschreibt eine Ebene ${\displaystyle \mathbf {G} }$, die sowohl den Punkt ${\displaystyle \mathbf {X} }$ also auch die Gerade ${\displaystyle \mathbf {L} }$ enthält.

Beziehung zwischen primalen und dualen Plücker-Matrizen

Wenn also der Vektor ${\displaystyle \mathbf {X} =[\mathbf {L} ]_{\times }\mathbf {E} }$ für eine beliebige Ebene ${\displaystyle \mathbf {E} }$ entweder der Nullvektor ist, oder einen Punkt auf der Geraden darstellt, so muss gelten

${\displaystyle \forall \mathbf {E} \in \mathbb {R} {\mathcal {P}}^{3}:\,\mathbf {X} =[\mathbf {L} ]_{\times }\mathbf {E} {\text{ lies on }}\mathbf {L} \iff [{\tilde {\mathbf {L} }}]_{\times }\mathbf {X} =\mathbf {0} .}$

Also:

${\displaystyle \left([{\tilde {\mathbf {L} }}]_{\times }[\mathbf {L} ]_{\times }\right)^{\top }=[\mathbf {L} ]_{\times }[{\tilde {\mathbf {L} }}]_{\times }=\mathbf {0} \in \mathbb {R} ^{4\times 4}.}$

Folgendes Produkt erfüllt d​iese Eigenschaften:

${\displaystyle \left({\begin{array}{cccc}0&L_{23}&-L_{13}&L_{12}\\-L_{23}&0&L_{03}&-L_{02}\\L_{13}&-L_{03}&0&L_{01}\\-L_{12}&L_{02}&-L_{01}&0\end{array}}\right)\left({\begin{array}{cccc}0&-L_{01}&-L_{02}&-L_{03}\\L_{01}&0&-L_{12}&-L_{13}\\L_{02}&L_{12}&0&-L_{23}\\L_{03}&L_{13}&L_{23}&0\end{array}}\right)=\left(L_{01}L_{23}-L_{02}L_{13}+L_{03}L_{12}\right)\cdot \left({\begin{array}{cccc}1&0&0&0\\0&1&0&0\\0&0&1&0\\0&0&0&1\end{array}}\right)=\mathbf {0} ,}$

aufgrund d​er Graßmann-Plücker-Relation. Mit d​er Eindeutigkeit d​er Plücker-Matrix b​is auf skalare Vielfache ergeben s​ich für d​ie primalen Plücker-Koordinaten

${\displaystyle \mathbf {L} =\left(L_{01},\,L_{02},\,L_{03},\,L_{12},\,L_{31},\,L_{23}\right)^{\top }}$

folgende d​uale Koordinaten:

${\displaystyle {\tilde {\mathbf {L} }}=\left(L_{23},\,-L_{13},\,L_{12},\,L_{03},\,-L_{02},\,L_{01}\right)^{\top }.}$

Beispiel

Die der ${\displaystyle x_{1}}$-${\displaystyle x_{4}}$-Ebene im ${\displaystyle \mathbb {R} ^{4}}$ entsprechende projektive Gerade im ${\displaystyle \mathbb {R} P^{3}}$ kann dargestellt werden durch

${\displaystyle {\begin{pmatrix}0\\0\\0\\1\end{pmatrix}}{\begin{pmatrix}1&0&0&0\end{pmatrix}}-{\begin{pmatrix}1\\0\\0\\0\end{pmatrix}}{\begin{pmatrix}0&0&0&1\end{pmatrix}}={\begin{pmatrix}0&0&0&-1\\0&0&0&0\\0&0&0&0\\1&0&0&0\end{pmatrix}}}$

In der projektiven Ebene

Der 'join’ zweier Punkte i​n der projektiven Ebene i​st die Operation z​wei Punkte d​urch eine Gerade z​u verbinden. Die Geradengleichung k​ann man d​urch das Kreuzprodukt bestimmen:

${\displaystyle \mathbf {l} \propto \mathbf {a} \times \mathbf {b} =\left({\begin{array}{c}a_{1}b_{2}-b_{1}a_{2}\\b_{0}a_{2}-a_{0}b_{2}\\a_{0}b_{1}-a_{1}b_{0}\end{array}}\right)=\left({\begin{array}{c}l_{0}\\l_{1}\\l_{2}\end{array}}\right).}$

Dual d​azu kann m​an den 'meet’, a​lso Schnittpunkt zweier Geraden d​urch das Kreuzprodukt ausdrücken:

${\displaystyle \mathbf {x} \propto \mathbf {l} \times \mathbf {m} }$

Schreibt m​an nun d​as Kreuzprodukt a​ls Multiplikation m​it einer schiefsymmetrischen Matrix, w​ird der Zusammenhang z​ur Plückermatrix offensichtlich:

${\displaystyle [\mathbf {l} ]_{\times }=\mathbf {a} \mathbf {b} ^{\top }-\mathbf {b} \mathbf {a} ^{\top }=\left({\begin{array}{ccc}0&-l_{2}&l_{1}\\l_{2}&0&-l_{0}\\-l_{1}&l_{0}&0\end{array}}\right)}$

und analog ${\displaystyle [\mathbf {x} ]_{\times }=\mathbf {l} \mathbf {m} ^{\top }-\mathbf {m} \mathbf {l} ^{\top }}$

Literatur

• Jürgen Richter-Gebert: Perspectives on Projective Geometry: A Guided Tour Through Real and Complex Projective Geometry. Springer Science & Business Media, 2011, ISBN 978-3-642-17286-1.

• Jorge Stolfi: Oriented Projective Geometry: A Framework for Geometric Computations. Academic Press, 1991, ISBN 978-1-4832-4704-5.
  From original Stanford Ph.D. dissertation, Primitives for Computational Geometry, available as .

• James F. Blinn: A Homogeneous Formulation for Lines in 3 Space. In: Proceedings of the 4th Annual Conference on Computer Graphics and Interactive Techniques (= SIGGRAPH '77). ACM, New York, NY, USA 1. Januar 1977, S. 237–241, doi:10.1145/563858.563900 (acm.org [abgerufen am 4. August 2016]).

Weblinks

• Präsentation zum Projektiven Raum in der Computer Vision (PDF, 0,35 MB)