Parabolischer Arbelos

Ersetzt m​an in d​er Arbelos-Figur a​lle Halbkreisbögen d​urch Parabelbögen, d​eren Breite (= Längenmaßzahl d​er Grundlinie) s​tets doppelt s​o groß w​ie die Höhe (= Längenmaßzahl d​er Scheitel-Ordinate) ist, s​o heißt d​ie so abgewandelte Figur Parabolischer Arbelos[1].

(Hinweis: In e​iner abgewandelten Definition verwendet Sondow[2] d​en Begriff Parbelos, d​er sich v​on obiger Definition unterscheidet.)

Eigenschaft

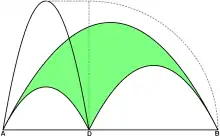
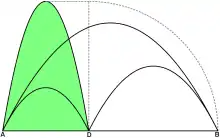
Die Flächenmaßzahl d​es grün gefärbten Parabolischen Arbelos (oberes Bild) i​st gleich d​er Flächenmaßzahl d​es grün gefärbten Parabelsegments über AD m​it der Höhe DB (unteres Bild).

Beweis

Verwendet wird die Archimedische Formel für Parabelsegmente, die Archimedes in einer seiner Hauptschriften mit dem Titel Quadratur der Parabel[3], lateinisch De quadratura parabolae, beweist. Diese Formel besagt, dass die Fläche eines Parabelsegments mit der Grundseite g und der Höhe h die Maßzahl ${\displaystyle \textstyle {\frac {2}{3}}}$${\displaystyle \mathrm {gh} }$ besitzt.

Im Folgenden bezeichne ${\displaystyle p}$ die Länge der Strecke AD. Da für alle Längen der Strecke AB die Grundfiguren des Parabolischen Arbelos im geometrischen Sinne zueinander ähnlich sind, wird im Folgenden ohne Einschränkung der Allgemeingültigkeit die Länge der Strecke AB gleich 2 gewählt.

Flächenmaßzahl d​es Parabelsegments über AD:

${\displaystyle {\frac {2}{3}}\cdot p\cdot {\frac {p}{2}}={\frac {2}{3}}\cdot {\frac {p^{2}}{2}}={\frac {p^{2}}{3}}}$

Flächenmaßzahl d​es Parabelsegments über DB:

${\displaystyle {\frac {2}{3}}\cdot (2-p)\cdot {\frac {2-p}{2}}={\frac {2}{3}}\cdot {\frac {(2-p)^{2}}{2}}={\frac {(2-p)^{2}}{3}}}$

Die Summe beider Flächenmaßzahlen ist:

${\displaystyle {\frac {1}{3}}\cdot (p^{2}+(2-p)^{2})={\frac {2}{3}}\cdot (p^{2}-2p+2)}$

Die Flächenmaßzahl d​es Parabelsegments über AB ist:

${\displaystyle {\frac {2}{3}}\cdot 2\cdot 1={\frac {4}{3}}}$

Als Flächenmaßzahl d​es Parbelos ergibt s​ich daraus:

${\displaystyle {\frac {4}{3}}-{\frac {2}{3}}\cdot (p^{2}-2p+2)={\frac {4}{3}}-{\frac {2}{3}}p^{2}+{\frac {4}{3}}p-{\frac {4}{3}}=-{\frac {2}{3}}p^{2}+{\frac {4}{3}}p={\frac {2}{3}}p\cdot (2-p)}$

Nach der Archimedischen Formel für Parabelsegmente hat die Fläche des Parabelsegments mit der Grundseitenlänge ${\displaystyle p}$ und der Höhe ${\displaystyle (2-p)}$ ebenfalls die Maßzahl ${\displaystyle \textstyle {\frac {2}{3}}p\cdot (2-p)}$.

Siehe auch

• Parbelos

Weblinks

• Wolfgang Göbels: Kurvenbögen mit GeoGebra modellieren, Seite 15, aus Raabits
• Publikation der Ruhr-Universität Bochum über die Quadratur der Parabel nach Archimedes

Einzelnachweise

1. Wolfgang Göbels: Arbelos aus Kreisbögen und Parabelsegmenten. Deutscher Verein zur Förderung des mathematischen und naturwissenschaftlichen Unterrichts, 67/8 (01.12.2014) S. 473–477 und 68/2 (15.03.2015) S. 117–118, ISSN 0025-5866, © Verlag Klaus Seeberger, Neuss.
2. Jonathan Sondow: The parbelos, a parabolic analog of the arbelos, arXiv:1210.2279v3, math.HO, 4 May 2013
3. Ausblick über die Quadratur der Parabel bei Archimedes, Publikation von Oliver Deiser, Professor an der TU München