Pandiagonales magisches Quadrat

Ein pandiagonales magisches Quadrat (manchmal auch panmagisch oder diabolisch genannt) ist ein magisches Quadrat, bei dem zusätzlich auch die gebrochenen Diagonalen die magische Summe ergeben.[1]

Gebrochene Diagonalen

Die gebrochenen Diagonalen verlaufen parallel zur Haupt- bzw. Nebendiagonalen und werden zyklisch betrachtet. Verlässt man also das Quadrat an einem Ende, verläuft die Diagonale auf der gegenüberliegenden Seite weiter.

1	8	13	12
14	11	2	7
4	5	16	9
15	10	3	6

1	8	13	12
14	11	2	7
4	5	16	9
15	10	3	6

Für die aufwärts verlaufenden gebrochenen Diagonalen gilt also

• 10+16+7+1 = 34
• 3+9+14+8 = 34
• 6+4+11+13 = 34

und ebenso für die abwärts gebrochenen verlaufenden Diagonalen

• 8+2+9+15 = 34
• 13+7+4+10 = 34
• 12+14+5+3 = 34

Verschiebungen

Die Verschiebung ist eine spezielle Tauschoperation bei magischen Quadraten mit pandiagonaler Eigenschaft. Durch die Verschiebung werden magische Quadrate innerhalb eines Verschiebungsclusters ineinander überführt. Da die gebrochenen Diagonalen auch die magische Summe ergeben, können beliebig viele Zeilen am oberen Rand des Quadrates abgetrennt und unten wieder angefügt werden. Ebenso können beliebig viele Spalten am linken Rand des Quadrates abgetrennt und am rechten Rand wieder angefügt werden. In allen Fällen entsteht wieder ein pandiagonales magisches Quadrat.

Horizontale und vertikale Verschiebungen in einem pandiagonalen magischen Quadrat

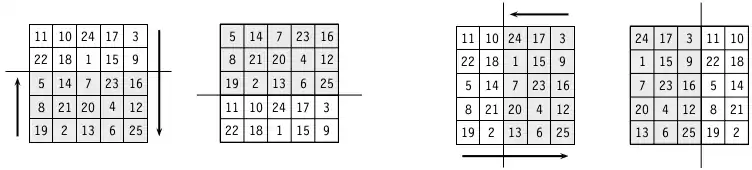
Durch eine Kombination der beiden Transformationen kann jede beliebige Zelle des magischen Quadrats in die linke obere Ecke verschoben werden, ohne dass die pandiagonale Eigenschaft verloren geht.

Beliebige Verschiebung in einem pandiagonalen magischen Quadrat

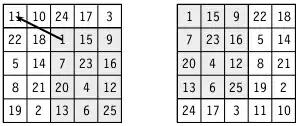
Wesentlich verschieden nennt man daher pandiagonale magische Quadrate, die durch keine Abbildung ineinander überführt werden können.

3x3 pandiagonale magische Quadrate

Es ist leicht zu überprüfen, dass es kein einziges pandiagonales Quadrat der Ordnung 3 gibt. Für höhere Ordnungen ist die genaue Anzahl teilweise bekannt oder lässt sich abschätzen.[2]

4x4 pandiagonale magische Quadrate

Insgesamt gibt es 48 pandiagonale magische Quadrate. Jeweils 16 magische Quadrate gehören zu einem der drei Verschiebungscluster. So können alle pandiagonalen magischen Quadrate der 4. Ordnung leicht gebildet werden.

1	8	13	12
14	11	2	7
4	5	16	9
15	10	3	6

1	12	7	14
8	13	2	11
10	3	16	5
15	6	9	4

1	8	11	14
12	13	2	7
6	3	16	9
15	10	5	4

Bei Verschiebung pandiagonaler magischer Quadrate der 4. Ordnung (SG 1) im Verschiebungscluster tritt keine Änderung der inneren Struktur ein. Das ist eine besondere Eigenschaft dieser Strukturgruppe. Die Herleitung dieser Eigenschaft am Strukturbild der Strukturgruppe 1 wird empfohlen.

Original und Komplement gehören bei pandiagonalen magischen Quadraten der 4. Ordnung (SG 1) zum selben Verschiebungscluster.

Die magische Summe 34 tritt in einem pandiagonalen Quadrat 4. Ordnung sehr häufig auf. Am Beispiel des linken Quadrats seien folgende Eigenschaften beispielhaft dargestellt:

• Die Summe der Zahlen in allen sechzehn 2x2-Teilquadraten ergibt 34, z. B. 1+8+14+11, 8+13+11+2 usw. Dabei können diese Teilquadrate auch zyklisch betrachtet werden, z. B. 12+7+1+14 oder 6+12+15+1.
• Die Summe der Ecken aller 3x3-Teilquadrate ergibt immer 34, z. B. 1+13+4+16 oder 8+12+5+9.
• Die diagonal gegenüberliegenden Ecken aller 3x3-Teilquadrate ergeben immer 34. Daher kann es kein symmetrisches pandiagonales Quadrat 4. Ordnung geben.
• Jedes Paar von horizontal oder vertikal benachbarten Zahlen ergibt mit den Zahlen, die sich zwei Zeilen tiefer und 2 Spalten weiter rechts befinden, addiert immer 34, z. B. 1+8+16+9 oder 1+14+16+3.

5x5 pandiagonale magische Quadrate

Im Unterschied zu der Ordnung 4 gibt es auch symmetrische pandiagonale Quadrate, da wie im folgenden Beispiel jede Zahl mit ihrer zum Zentrum symmetrischen liegenden Zahl addiert immer das Komplement n²+1 ergibt.[3]

1	15	22	8	19
23	9	16	5	12
20	2	13	24	6
14	21	10	17	3
7	18	4	11	25

Insgesamt gibt es 3600 pandiagonale Quadrate fünfter Ordnung, von denen aber nur 144 wesentlich verschieden sind. Ein sehr altes pandiagonales Quadrat aus dem arabischen Raum stammt aus dem 11. oder 12. Jahrhundert.[4] Die speziellen Eigenschaften eines pandiagonalen Quadrats waren allerdings noch nicht bekannt und wurden erst im 19. Jahrhundert von A. H. Frost analysiert.[5]

15	2	19	6	23
16	8	25	12	4
22	14	1	18	10
3	20	7	24	11
9	21	13	5	17

6x6 pandiagonale magische Quadrate

Es gibt kein pandiagonales magisches Quadrat 6. Ordnung. Der Nachweis wurde bereits 1878 von A. H. Frost geführt.[5] Ein weiterer eleganter Beweis stammt von C. Planck (1919).[6] Ganz allgemein existiert für keine einfach-gerade Ordnung n=4k+2 ein pandiagonales Quadrat.

7x7 pandiagonale magische Quadrate

Pandiagonale magische Quadrate dieser Ordnung sind sehr intensiv von Albert L. Candy untersucht worden.[7] Er fand heraus, dass es 678 222 720 pandiagonale Quadrate gibt, von denen 38 102 400 regulär und 640 120 320 irregulär sind.

1	28	39	9	48	19	31
46	16	34	5	24	36	14
27	40	10	43	21	32	2
17	29	7	25	37	13	47
42	11	44	20	33	3	22
30	6	26	38	8	49	18
12	45	15	35	4	23	41

1	43	40	32	28	18	13
24	20	9	2	47	38	35
46	42	31	26	16	8	6
15	12	4	49	39	33	23
41	30	22	19	11	7	45
14	3	48	37	29	27	17
34	25	21	10	5	44	36

8x8 pandiagonale magische Quadrate

Die Anzahl der pandiagonalen Quadrate 8. Ordnung ist nicht bekannt. Das nachfolgende Beispiel ist mit einem Algorithmus von Portier konstruiert worden.[8] Es ist nicht nur ein pandiagonales, sondern sogar ein cabalistisches magisches Quadrat und besitzt damit folgende Eigenschaften:

• es ist pandiagonal
• es ist bimagisch
• es besitzt trimagische Diagonalen
• das gesamte Quadrat kann in acht 2x4-Rechtecke aufgeteilt werden, deren Zahlen summiert immer 260 ergeben, z. B. 20+16+39+59+34+62+21+9 = 260

20	16	5	25	54	42	35	63
39	59	50	46	1	29	24	12
34	62	55	43	8	28	17	13
21	9	4	32	51	47	38	58
11	23	30	2	45	49	60	40
64	36	41	53	26	6	15	19
57	37	48	52	31	3	10	22
14	18	27	7	44	56	61	33

9x9 pandiagonale magische Quadrate

Pandiagonale Quadrate einer Ordnung, die ein Vielfaches von 3 sind, galten lange Zeit als unmöglich. Das erste bekannte Beispiel eines solchen Quadrates stammt von A. H. Frost aus dem Jahre 1878.[5]

57	80	67	12	8	22	48	44	31
10	9	23	46	45	32	55	81	68
47	43	33	56	79	69	11	7	24
62	76	66	17	4	21	53	40	30
18	5	19	54	41	28	63	77	64
52	42	29	61	78	65	16	6	20
58	75	71	13	3	26	49	39	35
14	1	27	50	37	36	59	73	72
51	38	34	60	74	70	15	2	25

Höhere Ordnungen und Konstruktion

Pandiagonale Quadrate höherer Ordnung lassen sich mit denselben Algorithmen erzeugen, wie Quadrate mit kleiner Ordnung. Dabei unterscheidet man Verfahren für folgende Ordnungen:

• ungerade Vielfache von 3 (9, 15, 21, …)
• ungerade, aber keine Vielfache von 3 (5, 7, 11, 13, 17, 19, 23, 25, …)
• doppelt-gerade (4, 8, 12, …)
• Primzahlen (5, 7, 11, 13, 17, 19, 23, 29, …)

Auch Online findet man Möglichkeiten zur Konstruktion von pandiagonalen magischen Quadraten.[9]

Einzelnachweise

1. Clifford A Pickover: The Zen of Magic Squares, Circles, and Stars. Princeton University Press, Princeton 2002, S. 68–77.
2. Enumeration of magic squares (englisch)
3. William H. Benson, Oswald Jacoby: New Recreations with Magic Squares. Dover-Publications, New York 1976, S. 49.
4. Schuyler Cammann: Islamic and Indian Magic Squares (Part I). In: History of Religions. Vol. 8, Nr. 3, 1969, S. 181–209.
5. A. H. Frost: On the General Properties of Nasik squares. In: The Quarterly Journal of Pure and Applied Mathematics. Vol. 15, 1878, S. 34–48.
6. C. Planck: Pandiagonal Magic squares of Order 6 and 10 with Minimal Numbers. In: The Monist. Vol. 29, 1919, S. 307–316.
7. Albert L. Candy: Pandiagonal magic squares of prime order. Selbstverlag, 1940.
8. Brutus Portier: Le Carré Cabalistique de 8. Librairie Adolphe Jourdan, Alger 1902.
9. Konstruktion von pandiagonalen magischen Quadraten

Weblinks

• Ausführliche Informationen und Konstruktion von magischen Quadraten
• Informationen über pandiagonale Quadrate (englisch)