Multiplikator-Akzelerator-Modell
Das Multiplikator-Akzelerator-Modell (oder auch manchmal Samuelson-Modell oder Samuelson-Hicks-Modell genannt) ist ein Konjunkturmodell. Es will erklären, warum das wirtschaftliche Wachstum nicht monoton verläuft, sondern typischerweise einem Konjunkturzyklus folgt. Das Modell lässt sich aus dem Wachstumsmodell von Harrod und Domar heraus entwickeln, eine besondere Variante stammt von Paul A. Samuelson und John Richard Hicks.
Formuliert man ein Harrod-Domar-Modell als zeitlich diskretes Modell und führt Verzögerungen in den Verhaltensgleichung ein, gelangt man zum Samuelson-Hicks-Modell, das die Abbildung von Konjunkturschwankungen erlaubt und das Volkseinkommen mit dem Konsum und Investition verbindet.
Ein einfaches Modell dieser Art kann zum Beispiel so aussehen:
- Konsumfunktion: mit
- Investitionsfunktion: mit v größer 0
dabei ist die Produktion bzw. die Gesamtnachfrage, der Konsum zum Zeitpunkt t, die Investitionen und steht hier für den „autonomen“, also konstanten Konsum.
Grundsätzlich können die zeitlichen Verzögerungen (Time lags) bei der Investitionsfunktion auch komplizierter gestaltet werden, außerdem kann auch der Konsum verzögert auf das Einkommen reagieren.
Beschreibung
Es handelt sich um ein keynesianisches Modell, das heißt, der Engpass ist die Nachfrage. Es wird angenommen, dass jede Nachfrage bedient werden kann, es gibt keine Angebotsengpässe. Die Nachfrage setzt sich zusammen aus der Nachfrage der Arbeiter nach Konsumgütern und der Nachfrage der Unternehmen nach Investitionsgütern. Je größer die Nachfrage, desto größer die Produktion, desto mehr Arbeitskräfte werden eingestellt, desto mehr Konsumgüter werden nachgefragt. Die Konsumnachfrage ist also ein bestimmter Teil c der Produktion und zwar der Vorperiode. Der Konsum reagiert also mit Verzögerung (Time-Lag) auf die Produktion. 1/(1-c) ist der „Multiplikator“ („Vervielfacher“), der angibt um das wievielfache eine bestimmte Erhöhung einer Nachfragegröße, beispielsweise der Investitionen, die Gesamtnachfrage erhöht.
Ähnlich wie beim Harrod-Domar-Modell kann die Nachfrage nach Investitionsgütern entweder als Anpassung an einen gewünschten Kapitalstock gedeutet werden oder als eine Investitionsfunktion, bei der die Investitionen durch die Veränderung der Nachfrage bestimmt werden.
Im Falle des „gewünschten Kapitalstocks“ steht dieser zur Nachfrage (der Vorperiode, er reagiert also mit zeitlicher Verzögerung) in einem bestimmten konstanten Verhältnis v (v ist der „Akzelerator“). Um vom tatsächlichen Kapitalstock zum gewünschten Kapitalstock zu kommen, muss die Differenz investiert werden. Die Unternehmen fragen also so viele Investitionsgüter nach, dass der alte Kapitalstock, nachdem er um die Investitionen zugenommen hat, gleich dem gewünschten Kapitalstock ist. Allerdings haben diese Investitionen als Teil der Nachfrage die Gesamtnachfrage erhöht, so dass der gewünschte Kapitalstock auch schon wieder größer geworden ist. Die Unternehmen versuchen also, mit dem "gewünschten Kapitalstock" ein sich bewegendes Ziel zu treffen. Durch die um einen Time lag verzögerte Reaktion auf die sich ständig verändernde Nachfrage kommen die Konjunkturschwankungen zustande.
Investitionen kleiner null sind als Abbau des Kapitalstocks zu deuten. Im einfachen Modell wird Symmetrie angenommen, Investitionen können beliebig größer oder kleiner null sein. Letztere Annahme müsste korrigiert werden, wenn die Verminderung des Kapitalstocks begrenzt ist durch die Abschreibungen.
v heißt deshalb Akzelerator („Beschleuniger“) und nicht Multiplikator, weil die Investitionen nicht einfach proportional zur Gesamtnachfrage sind, sondern proportional zur Veränderung der Nachfrage. Dieser Akzelerator ist in Verbindung mit Time lags, also mit zeitlichen Verzögerungen mathematisch für die Zyklen verantwortlich.
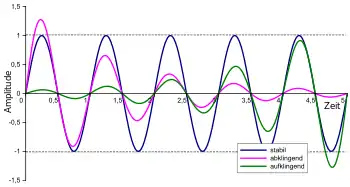
Es kann eine Fallunterscheidung vorgenommen werden je nach Größe der Parameter v und c. Folgende Fälle sind denkbar:
- exponentielles Wachstum
- exponentielles Schrumpfen
- explodierende Zyklen
- gedämpfte Zyklen
- als mathematischer Grenzfall: konstante Zyklen.
Konjunkturzyklen
Anfang
Aus diesen Annahmen ergeben sich Konjunkturzyklen. Steigt aus irgendeinem Grund die Nachfrage, steigt damit auch der Zielwert für den gewünschten Kapitalstock. Es muss mehr investiert werden. Damit kommt ein sich aufschaukelnder Aufschwung in Gang, da diese Investitionen ja auch wieder Nachfrage sind, die gesamtwirtschaftliche Nachfrage also erhöhen, also mehr Investitionen erforderlich machen usw.
Oberer Wendepunkt
Investitionen sind aber nicht nur Nachfrage, sie haben auch einen Kapazitätseffekt, sie erhöhen ja den Kapitalstock. Schließlich holt das Wachstum des Kapitalstocks das Wachstum der Nachfrage ein. Die Unternehmen müssen ihre Investitionen dann nicht mehr weiter ausdehnen. Tun das alle Unternehmen, steigt die Nachfrage nach Investitionsgütern nicht weiter. Der Kapitalstock wächst aber weiterhin, eben in Höhe der immer noch getätigten Investitionen. Es öffnet sich jetzt eine Schere zwischen weiter wachsendem Kapitalstock und nachlassendem Nachfragewachstum. Es liegt eine Überinvestitions- und Überakkumulationskrise mit unterausgelasteten Produktionskapazitäten vor. Diese Krise leitet in den Abschwung über. Den Investitionen wohnt also ein Widerspruch inne. Ein bestimmtes jährliches Investitionsvolumen stellt Jahr für Jahr eine bestimmte konstante Nachfrage dar. Es verändert aber Jahr für Jahr die Angebotskapazitäten, es erhöht sie jährlich um eben seinen Betrag. Eine „Überangebotskrise“ ist somit programmiert.
Abschwung
Der Kapitalstock ist jetzt zu groß, es wird weniger investiert. Ein sich selbst verstärkender Abschwung beginnt. Je weniger investiert wird, desto geringer die gesamtwirtschaftliche Nachfrage, desto niedriger der gewünschte Kapitalstock, desto weniger wird investiert. Die Investitionen reichen schließlich nicht mehr aus, um den Verschleiß der Produktionskapazitäten auszugleichen. Produktionskapazitäten werden stillgelegt. Der Kapitalstock schrumpft. Außerdem entsteht eine Pleitewelle. Die aus dem Markt scheidenden Unternehmen tragen auch zum Schrumpfen des Kapitalstocks bei.
Unterer Wendepunkt
Schließlich hält das Schrumpfen des Kapitalstocks mit der fallenden Nachfrage Schritt. Die Pleitewelle hält an, dehnt sich aber nicht weiter aus. Damit wird die Nachfrage auf niedrigem Niveau stabilisiert, während infolge der ja noch anhaltenden Pleitewelle die Produktionskapazitäten weiterhin schrumpfen. Es öffnet sich jetzt eine Schere zwischen weiter schrumpfendem Kapitalstock und sich stabilisierender Nachfrage. Fehlenden Investitionen wohnt also auch ein Widerspruch inne. Sie lassen die Nachfrage unverändert, bewirken aber, dass die Angebotskapazitäten um eben die fehlenden Investitionen jährlich schrumpfen. Eine „Unterangebotskrise“ ist programmiert, die Investitionen auslöst, die in den Aufschwung überleiten.
Aufschwung
Die Produktionskapazitäten sind jetzt zu hoch ausgelastet. Es muss wieder mehr investiert werden. Dies führt zu wieder steigender Nachfrage, die Investitionen steigen daher noch mehr, es entsteht ein sich selbst verstärkender Aufschwung, weiter siehe oben.
Mathematisch wird jedes Mal der gesamte Kapitalstock, der im Aufschwung aufgebaut wurde, im Abschwung in einer Reinigungskrise wieder zerstört.
Rechnerisches Beispiel
Fallunterscheidung
Für dieses Gleichungssystem kann folgende Fallunterscheidung getroffen werden[1]:
- v < s: gedämpfte Schwingungen
- s = v: konstante Schwingungen
- s < v < 4s: explodierende Schwingungen
- v > oder = 4s: stetiges Wachstum
Für andere Gleichungen ergäben sich andere Fallunterscheidungen.
 Gedämpfte Schwingung: s=0,6, v=0,5
Gedämpfte Schwingung: s=0,6, v=0,5 Explodierende Schwingungen: s=0,45, v=0,5
Explodierende Schwingungen: s=0,45, v=0,5 Stetiges Wachstum: s=0,125, v=0,5
Stetiges Wachstum: s=0,125, v=0,5
Zahlenbeispiel (Fall konstante Schwingung s=v)
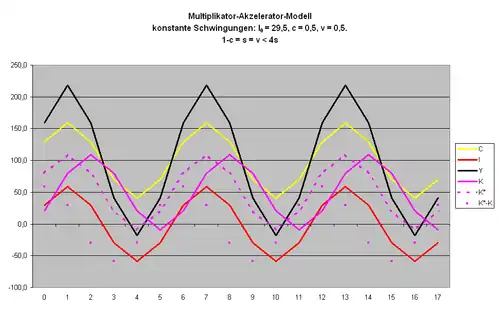
Für dieses Gleichungssystem ergeben sich konstante Schwingungen, wenn für c und v folgende Werte angesetzt werden:
Anfangsbedingung:
Für ergibt sich 129,5 und für 159,0.
Der Kapitalstock K ergibt sich, indem die Investitionen I aufkumuliert werden:
Version Anpassung an gewünschten Kapitalstock
Statt über die Investitionsfunktion kann das Modell auch als Anpassung an einen gewünschten Kapitalstock gedeutet werden.
Der gewünschte Kapitalstock sei:
ist die Abweichung des gewünschten Kapitalstocks vom tatsächlichen Kapitalstock. Wird dieser Wert investiert, kann sozusagen die Lücke zwischen Wunsch und Wirklichkeit geschlossen werden. Beim Multiplikator-Akzelerator-Modell wird von einer mit einem Time lag verzögerten Reaktion der Investitionen ausgegangen:
Setzt man als Anfangswert , erhält man mathematisch genau dieselben Investitionen, wie sie sich im oberen Modell ergäben, wo unmittelbar eine Investitionsfunktion, die direkt von der Veränderung der Produktion Y abhängt, angesetzt wurde. Andernfalls ergibt sich ein um eine konstante Größe verschiedenes Ergebnis. Mathematisch unterscheiden sich also die beiden Modelle, bis auf eine Konstante, nicht.
Wird das Gleichungssystem anders spezifiziert, ergeben sich andere Bedingungen für konstante Schwingungen.
Weitere Anwendungen
Das Multiplikator-Akzelerator-Modell kann auch dazu dienen, ähnliche Vorgänge abzubilden, etwa einen gesamtwirtschaftlichen Lagerzyklus, wenn angenommen wird, dass im Vergleich zum Bruttoinlandsprodukt ein bestimmtes Niveau an Lagerbeständen, oder wenn im Vergleich zum Bruttoinlandsprodukt eine bestimmte Höhe der Staatsverschuldung angestrebt wird. Im letzteren Fall entspräche der staatliche Schuldenstand dem Kapitalstock, der Finanzierungssaldo des Staates entspräche den Investitionen, wobei, ähnlich wie die Investitionen Teil des Bruttoinlandsprodukts sind, der staatliche Finanzierungssaldo das Bruttoinlandsprodukt verändert.
Literatur
- Roy G. D. Allen: Macro-Economic Theory. A Mathematical Treatment. Macmillan, London u. a. 1968.
Einzelnachweis
- Allen: Macro-Economic Theory. 1968, S. 335.