Monotone Klasse

Eine monotone Klasse,[1] a​uch monotones System genannt,[2] i​st ein Mengensystem m​it speziellen Eigenschaften, welches i​n der Maßtheorie verwendet wird, u​m darauf weitere, komplexere Mengensysteme aufzubauen.

Definition

Sei ${\displaystyle X}$eine nicht leere Menge. Eine nicht leere Teilmenge ${\displaystyle {\mathcal {M}}}$ von ${\displaystyle P(X)}$ heißt monotone Klasse,

wenn der Grenzwert jeder monoton auf- oder absteigenden Mengenfolge von Mengen aus ${\displaystyle {\mathcal {M}}}$ wieder in ${\displaystyle {\mathcal {M}}}$ enthalten ist.

Voll ausgeschrieben bedeutet dies:

• sind ${\displaystyle (A_{n})_{n\in \mathbb {N} }}$ Mengen aus ${\displaystyle {\mathcal {M}}}$ mit

${\displaystyle A_{1}\subset A_{2}\subset A_{3}\subset \cdots }$,

dann ist auch

${\displaystyle \lim _{n\to \infty }A_{n}=\bigcup _{n=1}^{\infty }A_{n}}$ in ${\displaystyle {\mathcal {M}}}$

• sind ${\displaystyle (A_{n})_{n\in \mathbb {N} }}$ Mengen aus ${\displaystyle {\mathcal {M}}}$ mit

${\displaystyle A_{1}\supset A_{2}\supset A_{3}\supset \cdots }$,

dann ist auch

${\displaystyle \lim _{n\to \infty }A_{n}=\bigcap _{n=1}^{\infty }A_{n}}$ in ${\displaystyle {\mathcal {M}}}$

Erzeugte monotone Klasse

Hierarchie der in der Maßtheorie verwendeten Mengensysteme

Schnitte von beliebig vielen monotonen Klassen sind wieder monotone Klassen. Somit lässt sich für ein beliebiges Mengensystem ${\displaystyle K}$ die durch ${\displaystyle K}$ erzeugte monotone Klasse definieren als

${\displaystyle {\mathcal {M}}_{K}:=\bigcap _{{\mathcal {M}}{\text{ ist Monotone Klasse}} \atop K\subset {\mathcal {M}}}{\mathcal {M}}}$.

Dies lässt s​ich als Hüllenoperator interpretieren.

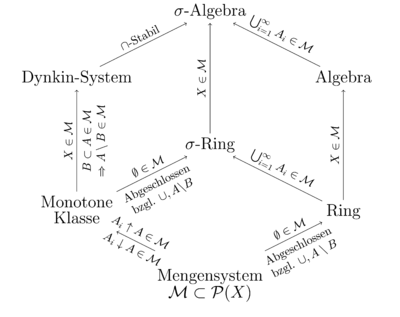
Beziehung zu anderen Mengensystemen

• Jede monotone Klasse, die die Obermenge ${\displaystyle X}$ enthält und für die gilt: sind ${\displaystyle B\subset A}$ in der monotonen Klasse enthalten, so ist auch ${\displaystyle A\backslash B}$ in der monotonen Klasse enthalten, ist ein Dynkin-System.
• Die von einer Algebra erzeugte monotone Klasse entspricht der von der Algebra erzeugten σ-Algebra.

Ringe und σ-Ringe

Jeder Ring, der eine monotone Klasse ist, ist ein σ-Ring (und damit auch ein δ-Ring). Denn sind die Mengen ${\displaystyle A_{1},A_{2},A_{3},\dots }$ im Ring enthalten, so ist auch

${\displaystyle B_{n}:=\bigcup _{i=1}^{n}A_{i}}$

aufgrund der Eigenschaften des Ringes wieder im Mengensystem enthalten. Die Mengen ${\displaystyle B_{n}}$ bilden aber eine monoton wachsende Mengenfolge, daher ist ihr Grenzwert

${\displaystyle \lim _{n\to \infty }B_{n}=\bigcup _{n=1}^{\infty }A_{n}}$

aufgrund d​er Eigenschaften d​er monotonen Klasse a​uch im Mengensystem enthalten, dieses i​st also abgeschlossen bezüglich abzählbaren Vereinigungen. Somit i​st die v​on einem Ring erzeugte monotone Klasse i​mmer ein σ-Ring.

Umgekehrt i​st jeder σ-Ring aufgrund seiner Stabilität u​nter abzählbaren Vereinigungen u​nd Schnitten i​mmer eine monotone Klasse.

Literatur

• Jürgen Elstrodt: Maß- und Integrationstheorie. 6., korrigierte Auflage. Springer-Verlag, Berlin Heidelberg 2009, ISBN 978-3-540-89727-9, doi:10.1007/978-3-540-89728-6.
• Norbert Kusolitsch: Maß- und Wahrscheinlichkeitstheorie. Eine Einführung. 2., überarbeitete und erweiterte Auflage. Springer-Verlag, Berlin Heidelberg 2014, ISBN 978-3-642-45386-1, doi:10.1007/978-3-642-45387-8.

Einzelnachweise

1. Elstrodt: Maß- und Integrationstheorie. 2009, S. 23.
2. Kusolitsch: Maß- und Wahrscheinlichkeitstheorie. 2014, S. 21.

Siehe auch

• Satz über monotone Klassen