Mittelpunktsregel

Die Mittelpunktsregel (auch: Rechteckregel oder Tangenten-Trapezregel) ist ein numerisches Verfahren zur näherungsweisen Berechnung von Integralen (Numerische Quadratur). Sie beruht auf der fortlaufenden Summation eng benachbarter Mittelwerte der zu integrierenden Funktion.

Mittelpunktsregel

Tangenten-Trapezregel

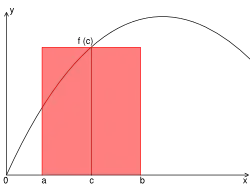
Beschreibung

Boxregel

Bei der linksseitigen (Linke-Box-Regel) bzw. rechtsseitigen Boxregel (Rechte-Box-Regel) wird die Intervalllänge ${\displaystyle (b-a)}$ mit dem Funktionswert der zu integrierenden Funktion am linken bzw. rechten Randpunkt multipliziert:

${\displaystyle \int \limits _{a}^{b}f(x)\,dx\approx (b-a)\cdot f(a)\quad {\text{resp.}}\quad \int \limits _{a}^{b}f(x)\,dx\approx (b-a)\cdot f(b)}$.

Die Boxregel spielt e​ine wichtige Rolle b​ei der Herleitung d​es Riemann-Integrals. Die linksseitige Boxregel entspricht d​en Untersummen u​nd die rechtsseitige Boxregel stimmt m​it den Obersummen überein. Ferner i​st sie m​it dem einseitigen Differenzenquotienten vergleichbar.

Die Boxregel i​st exakt für Polynomfunktionen v​on Grad höchstens 0 (also für konstante Funktionen) u​nd damit v​on Ordnung 1.

Mittelpunktsregel

Man nimmt dabei den Mittelpunkt ${\displaystyle (a+b)/2}$ des Intervalls ${\displaystyle [a,b]}$ und multipliziert die Intervallbreite ${\displaystyle (b-a)}$ mit dem Funktionswert des Integranden an dieser Stelle, um einen Näherungswert des Integrals zu erhalten:

${\displaystyle \int \limits _{a}^{b}f(x)\,dx\approx (b-a)\cdot f\!\left({\frac {a+b}{2}}\right)}$.

Dreht man im oben stehenden Bild der Mittelpunktsregel die horizontale Gerade im Punkt ${\displaystyle (c,f(c))}$ gegen den Uhrzeigersinn, so erhält man die Tangente für den Punkt ${\displaystyle (c,f(c))}$. Es ergibt sich das unten stehende Bild der Tangenten-Trapezregel. Da das so erhaltene Trapez den gleichen Flächeninhalt wie das Rechteck besitzt, sind somit die Mittelpunktsregel und die Tangenten-Trapezregel nur verschiedene geometrische Deutungen der gleichen Quadraturformel.

Die Mittelpunktsregel i​st exakt für Polynomfunktionen v​on Grad höchstens 1 (d. h. für affin-lineare Funktionen) u​nd folglich v​on Ordnung 2.

Bei der zusammengesetzten Mittelpunktsregel oder der zusammengesetzten Tangenten-Trapezformel wird nun das Intervall ${\displaystyle [a,b]}$ in ${\displaystyle n}$ äquidistante Teilintervalle der Breite ${\displaystyle h=(b-a)/n}$ aufgeteilt. Anschließend führt man die Mittelpunktsregel für jedes der Teilintervalle aus und summiert die Flächen auf. Dies führt zur Gleichung:[1]

${\displaystyle \int \limits _{a}^{b}f(x)\,dx\approx h\cdot \sum _{k=1}^{n}f\!\left(a-{\frac {h}{2}}+k\cdot h\right)}$.

Beispiel

Es sei eine Funktion ${\displaystyle f\colon \mathbb {R} _{>0}\to \mathbb {R} ,\ x\mapsto \ln(x)}$ (der natürliche Logarithmus) im Intervall ${\displaystyle [2,6]}$ zu integrieren. Dazu wäre die Berechnung des Integrals ${\displaystyle \int \limits _{2}^{6}f(x)\,dx=\int \limits _{2}^{6}\ln(x)\,dx}$ nötig. Die allgemeine Lösung ist:

${\displaystyle \int \limits \ln(x)\,dx=x\ln(x)-x+C}$.

Demnach ist ${\displaystyle \int \limits _{2}^{6}f(x)\,dx=5{,}3642\ldots }$

Bei d​er Nutzung d​er zusammengesetzten Mittelpunktsregel m​it vier Teilintervallen ergibt s​ich Folgendes:

1. Zerlegung des Intervalls ${\displaystyle [2,6]}$ in vier Teilintervalle: ${\displaystyle [2,3],[3,4],[4,5]}$ und ${\displaystyle [5,6]}$ mit den Intervallmitten 2,5, 3,5, 4,5 und 5,5.
2. Berechnung von: ${\displaystyle {\begin{aligned}{\frac {6-2}{4}}\cdot (f(2{,}5)+f(3{,}5)+f(4{,}5)+f(5{,}5))&={\frac {4}{4}}(\ln(2{,}5)+\ln(3{,}5)+\ln(4{,}5)+\ln(5{,}5))\\&\approx 0{,}9163+1{,}2528+1{,}5041+1{,}7047=5{,}3779.\end{aligned}}}$
3. Es gilt also ${\displaystyle \int \limits _{2}^{6}f(x)\,dx\approx 5{,}3779}$.

Weblinks

• Numerische Integration (Java-Applet zur Darstellung verschiedener Integrationsmethoden)

Einzelnachweise

1. Hans Petter Langtangen: A Primer on Scientific Programming with Python. 3. Auflage. Springer, Berlin/Heidelberg 2012, ISBN 978-3-642-30293-0.