Meta-Tic-Tac-Toe
Meta-Tic-Tac-Toe ist ein Brettspiel, das aus neun Tic-Tac-Toe-Brettern besteht, die in einem 3 × 3-Raster angeordnet sind. Die Spieler spielen abwechselnd auf den kleineren Tic-Tac-Toe-Brettern, bis einer von ihnen auf dem größeren Tic-Tac-Toe-Brett gewinnt. Im Vergleich zu herkömmlichem Tic-Tac-Toe ist die Strategie in diesem Spiel konzeptionell schwieriger und hat sich für Computer als herausfordernder erwiesen.[1]
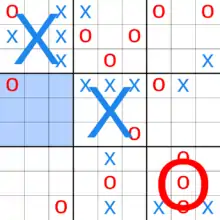
Regeln
Es wird auf einem Brett mit 9×9 Feldern gespielt, das in neun kleinere lokale Bretter von 3×3 Feldern eingeteilt ist. Die Spieler, X und O, ziehen abwechselnd, X beginnt. Der Spieler am Zug trägt sein Symbol in ein noch freies Feld ein (setzt in dieses Feld).
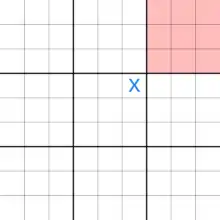
Der Startspieler kann sein erstes Symbol in ein beliebiges Feld eintragen. Danach muss jeder Zug in dem lokalen Brett gesetzt werden, das durch die Position des vorhergehenden Zuges in dessen lokalem Brett gegeben ist. Wenn z. B. in das obere rechte Feld eines lokalen Bretts gesetzt wird, muss der nächste Zug im oberen rechten lokalen Brett erfolgen. Der ziehende Spieler kann also nur wählen, in welches freie Feld des gegebenen lokalen Bretts er setzt.
Wenn ein Spieler in einem lokalen Brett eine Dreierreihe seiner Symbole (waagerecht, senkrecht oder diagonal) bildet, hat er damit dieses lokale Brett gewonnen, und in dieses darf dann nicht mehr gesetzt werden. Wenn das durch den vorhergehenden Zug gegebene lokale Brett bereits von einem Spieler gewonnen wurde oder voll besetzt ist, kann der Folgezug in ein beliebiges anderes noch nicht gewonnenes lokales Brett gesetzt werden.
Ziel des Spiels ist es, drei lokale Bretter zu gewinnen, die ihrerseits auf dem globalen Brett eine waagerechte, senkrechte oder diagonale Reihe bilden. Wenn keine Züge mehr möglich sind und kein Spieler die Siegbedingung erfüllt hat, endet das Spiel unentschieden.[2]
Spielweise
Meta-Tic-Tac-Toe ist wesentlich komplexer als die meisten anderen Variationen von Tic-Tac-Toe, da es keine klare Strategie für das Spielen gibt. Dies liegt an der komplizierten Spielverzweigung in diesem Spiel. Obwohl jeder Zug auf einem lokalen Brett gespielt werden muss, das einem normalen Tic-Tac-Toe-Brett entspricht, muss jeder Zug das globale Brett auf verschiedene Weise berücksichtigen:
- Den nächsten Zug vorwegnehmen: Jeder Zug, der auf einem lokalen Brett gespielt wird, bestimmt, wo der nächste Zug des Gegners gespielt werden darf. Dies kann dazu führen, dass Bewegungen, die im normalen Tic-Tac-Toe-Bereich als schlecht angesehen werden, realisierbar sind, da der Gegner an ein anderes lokales Brett geschickt wird und möglicherweise nicht sofort auf den gemachten Zug reagieren kann. Daher sind die Spieler gezwungen, das größere Spielbrett in Betracht zu ziehen, anstatt sich nur auf das lokale Brett zu konzentrieren.
- Vorhersehen der Zugfolgen: Das Visualisieren zukünftiger Zweige des Spielbaums ist schwieriger als das Einbrett-Tic-Tac-Toe. Jede Bewegung bestimmt die nächste Bewegung, und daher folgt die Vorhersehung zukünftige Bewegungen einem viel weniger linearen Pfad. Zukünftige Positionen sind nicht mehr austauschbar, jeder Schritt führt zu stark unterschiedlichen möglichen zukünftigen Positionen. Dies macht es schwierig, den Spielbaum zu visualisieren, wodurch möglicherweise viele mögliche Pfade übersehen werden. Auf gegnerische Züge kann möglicherweise nicht sofort reagiert werden. Daher sind die Spieler gezwungen, das größere Spielbrett in Betracht zu ziehen, anstatt sich nur auf das lokale Brett zu konzentrieren.
- Das Spiel gewinnen: Aufgrund der Regeln des Meta-Tic-Tac-Toe ist das globale Brett niemals direkt betroffen. Es wird nur durch Aktionen beeinflusst, die auf lokalen Brettern stattfinden. Dies bedeutet, dass jeder gespielte lokale Zug nicht dazu gedacht ist, das lokale Brett, sondern das globale Brett zu gewinnen. Lokale Gewinne sind nicht wertvoll, wenn sie nicht zum Gewinnen des globalen Bretts verwendet werden können. Tatsächlich kann es strategisch sein, dem Gegner ein lokales Brett zu opfern, um selbst ein wichtigeres lokales Brett zu gewinnen. Diese zusätzliche Komplexität macht es für den Menschen schwieriger, die relative Wichtigkeit und Bedeutung von Bewegungen zu analysieren, und folglich ist es schwieriger, gut zu spielen.
Computerimplementierungen
Während Tic-Tac-Toe elementar zu lösen ist und fast sofort mit der Tiefensuche durchgeführt werden kann, kann das Meta-Tic-Tac-Toe mit keiner Brute-Force-Taktik vernünftigerweise gelöst werden. Daher sind kreativere Computerimplementierungen erforderlich, um dieses Spiel zu spielen.
Die gebräuchlichste Taktik der künstlichen Intelligenz (KI), Minimax, kann verwendet werden, um Meta-Tic-Tac-Toe zu spielen, hat jedoch Schwierigkeiten, dies zu spielen. Das liegt daran, dass dem Meta-Tic-Tac-Toe trotz relativ einfacher Regeln eine einfache heuristische Bewertungsfunktion fehlt. Diese Funktion ist im Minimax erforderlich, da sie bestimmt, wie gut eine bestimmte Position ist. Obwohl elementare Bewertungsfunktionen für das Meta-Tic-Tac-Toe unter Berücksichtigung der Anzahl lokaler Siege erstellt werden können, übersehen diese weitgehend den Positionsvorteil, der viel schwieriger zu quantifizieren ist. Ohne eine effiziente Bewertungsfunktion sind die meisten typischen Computerimplementierungen schwach, und daher gibt es nur wenige Computergegner, die Menschen konsequent übertreffen können.
Algorithmen der künstlichen Intelligenz, die keine Bewertungsfunktionen benötigen, wie der Monte-Carlo-Baumsuchalgorithmus, haben jedoch kein Problem beim Spielen dieses Spiels. Die Monte-Carlo-Baumsuche basiert auf zufälligen Simulationen von Spielen, um zu bestimmen, wie gut eine Position ist, und kann daher genauer beurteilen, wie gut eine aktuelle Position ist. Daher übertreffen Computerimplementierungen, die diese Algorithmen verwenden, Minimax-Lösungen und können menschliche Gegner konsequent schlagen.[3]
Weblinks
Einzelnachweise
- Eytan Lifshitz, David Tsurel: AI Approaches to Ultimate Tic-Tac-Toe. In: The Rachel and Selim Benin School of Computer Science and Engineering. 26. Dezember 2016.
- Ben Orlin: Ultimate Tic-Tac-Toe. In: Math with Bad Drawings. 16. Juni 2013. Abgerufen am 18. Oktober 2016.
- Ofek Gila: What is the Monte Carlo tree search?. In: We Blog. 27. Juni 2016. Abgerufen am 18. Oktober 2016.