Münsterberg-Täuschung
Die Münsterberg-Täuschung ist eine visuelle Wahrnehmungstäuschung, bei der zwei parallele vertikale Reihen von schwarzen Quadraten auf hellem Hintergrund als geneigt im Vergleich zur Lotrechten wahrgenommen werden, wenn sie gegeneinander verschoben und die Quadrate durch vertikale Linien miteinander verbunden sind. Sie ist nach ihrem Entdecker Hugo Münsterberg benannt.
Geschichte
Die Täuschung wurde 1897 von Hugo Münsterberg[1] veröffentlicht, in der er berichtet, er habe sie „nicht auf dem Wege theoretischer Erwägungen gefunden, sondern durch Betrachtungen einer amerikanischen Pferdebahnabonnementskarte“. Er konstruierte auch eine mechanische Vorrichtung, an der die Täuschung experimentell variiert werden konnte. Pierce[2] untersuchte den Einfluss des Irradiationseffekts. Fraser[3] prägte den Begriff „unit of direction“ (etwa: Richtungselement) für je zwei durch eine Linie verbundene schwarze Quadrate links und rechts der Figurenachse (Bild 3). Eine so definierte geometrische Einheit weist C2 -Symmetrie auf. Mehrere Varianten des Stimulus wurden von Kitaoka, Pinna und Brelstaff[4] veröffentlicht und eingehend untersucht.
Der Stimulus

Je zwei schwarze Quadrate grenzen aneinander, sind jedoch um eine halbe Seitenlänge verschoben. Die vertikalen Abstände zwischen den schwarzen Quadraten entsprechen ihrer Seitenlänge, so dass die hellen Bereiche dazwischen ebenfalls als Quadrate wahrgenommen werden. Entlang der Figurenachse verlaufen Linien, die zum einen je zwei schwarze Quadrate auf gegenüber liegenden Seiten der Achse verbinden, aber gleichzeitig die weißen Quadrate trennen.
Beobachtung
Die schwarzen Linien zwischen einem Quadrat und dem jeweils nächsten suggerieren eine zwischen den beiden Reihen von Quadraten durchgehend verlaufende Linie. Diese erscheint im Uhrzeigersinn geneigt gegen die Vertikale und die gesamte Figur wirkt gekippt. Entsprechend scheinen die an die Mittellinie angrenzenden Seiten der Quadrate nicht mehr exakt parallel zu deren Außenseiten. Die Täuschung wird am besten wahrgenommen, wenn man den gesamten Stimulus ins Auge fasst und den Blick auf eine Stelle etwas seitlich von der Figur richtet. Die Intensität der Täuschung verringert sich, wenn man nur auf einen kleinen Ausschnitt fixiert. Eine Drehung um beliebige Winkel ändert den Eindruck nicht wesentlich. Die Täuschung verschwindet, wenn die schwarzen Verbindungslinien fehlen oder auch nur eine der beiden vertikalen Reihen von schwarzen Quadraten seitlich ein wenig von der Mittellinie abgerückt wird. Der Effekt zeigt sich in gleicher Intensität an der Figur in Weiß auf schwarzem Grund.
Unterschied zur Café Wall Illusion

In der Münsterberg-Täuschung sind nur zwei Reihen von rein schwarzen Quadraten auf hellem Grund zu sehen, zwischen denen eine schwarze Linie verläuft, während die Café Wall Illusion aus mehreren, durch graue Linien getrennten Reihen von Rechtecken besteht. Sie wird auch manchmal als die allgemeinere Form der Münsterberg-Täuschung bezeichnet.
Deutungen
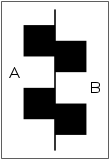
- Nach Münsterberg entsteht die Täuschung durch Irradiation. Danach erscheint ein helles Quadrat in schwarzer Umgebung größer als umgekehrt. Zur Erklärung greift man in Bild 1 einen Abschnitt heraus (Bild 2), in dem zwei helle als Quadrate wahrgenommene Bereiche durch die schwarze Linie voneinander getrennt sind. Das linke, etwas höher liegende Quadrat (A), grenzt rechts oben mit zwei Seiten an schwarze Flächen. Dort werde es, so der Autor, infolge des Irradiationseffekts vergrößert wahrgenommen: „Die Hauptwirkung der Irradiation liegt offenbar darin, dass das weiße Quadrat nicht bloß seine rechtwinkelige Form über die Mittellinie hinausschiebt, sondern sich scheinbar mit spitzem Winkel in das schwarze Doppelquadrat hineinbohrt.“ Etwas tiefer leistet das rechte weiße Quadrat (B) dasselbe in Richtung nach links unten und deshalb wird die Schwarz-Weiß-Grenze als im Uhrzeigersinn gekippt wahrgenommen. Die Linie bleibe jedoch unverändert, wo auf beiden Seiten weiße Flächen zu sehen sind. Der sich wiederholende Effekt an den einzelnen Abschnitten summiert sich zu einer Neigung der gesamten Figur.
- Kitaoka ergänzt diese Deutung, indem er denselben Effekt auch für die schwarzen Quadrate postuliert und ihn auch auf nicht rechte Winkel ausdehnt.[5] Kitaoka, Pinna und Brelstaff erklären die Richtung der wahrgenommenen Neigung mit dem Mechanismus der „Contrast polarities“.[6]

- Einfluss virtueller Linien. Danach hat die Wahrnehmung die Tendenz, Bereiche gleicher empfundener Helligkeit durch virtuelle Linien miteinander zu verbinden. Beispiele sind das Kanizsa-Dreieck oder die Café Wall Illusion.[7] Bereits Kitaoka, Pinna und Brelstaff (2004) diskutierten einen möglichen Effekt räumlicher Filterung im Verlauf des Wahrnehmungsprozesses. Die Münsterberg-Figur wird, wie schon von Fraser (1908) vorgeschlagen, gedanklich in einzelne sich wiederholende Abschnitte zerlegt (Bild 3). Diese besitzen C2-Symmetrie und geben eine Richtung schräg zur Figurenachse vor. Die Wahrnehmung ersetzt die geometrische Einheit durch eine virtuelle Linie, die in Richtung der kürzesten Verbindung zwischen den optischen Schwerpunkten der Quadrate geneigt ist (rote Linie in Bild 3). Diese tritt in Wechselwirkung mit der wirklichen Linie, die die Quadrate über ihre Ecken an den Innenseiten verbindet. Diese erscheint dann ebenfalls gekippt. In der Summe führt das zu einer scheinbaren Drehung der ganzen Figur im Uhrzeigersinn.[8]
Varianten
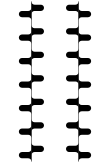
Die Grundform, von Münsterberg an verschobenen Quadraten beobachtet, lässt sich in vielfältiger Weise abändern, ohne dass die Täuschung verschwindet. Eine dieser Varianten – mit sowohl schwarzen wie auch weißen Verbindungsstrichen – besteht aus gerundeten Elementen (Bild 4).
Vergleichbare Täuschungen
- Ein ähnlicher Effekt ist auch beim „Twisted cord“ von Fraser (1908) zu erkennen.
- Gregory und Heard[9] publizierten die Café Wall Illusion. An die Stelle der Quadrate treten hier Rechtecke, die, abwechselnd in Schwarz und Weiß, in mehreren horizontalen Reihen angeordnet sind. Wie bei der Münsterberg-Täuschung wird die Trennlinie zwischen den Reihen als geneigt gegen ihren geometrischen Verlauf empfunden, es tritt jedoch auch die scheinbare Trapezform der einzelnen Elemente stärker hervor. Die Café Wall illusion wird bisweilen auch als die allgemeine Form der Münsterberg-Täuschung bezeichnet.
- Auch in der Zöllner-Täuschung sind Linien scheinbar im Vergleich zu ihrem tatsächlichen Verlauf geneigt.
- Wade (1982)[10] wie auch Kitaoka (1998) bringen zweidimensionale Beispiele, in denen gerade Linien gekrümmt oder parallele Linien gegeneinander geneigt erscheinen.
Einzelnachweise
- H. Münsterberg: Die verschobene Schachbrettfigur. In: Zeitschrift für Psychologie. 5, 1897, S. 185–188.
- A. H. Pierce: The illusion of the kindergarten patterns. In: Psychological Review. 5, 1898, S. 233–253.
- J. Fraser: A New Visual Illusion of Direction. In: British Journal of Psychology. 2, 1908, S. 307–320.
- A. Kitaoka, B. Pinna, G. Brelstaff: Last but not least. In: Perception. 30, 2001, S. 637–646.
- A. Kitaoka: Apparent contraction of edge angles. In: Perception. 27, 1998, S. 1209–1219.
- A. Kitaoka, B. Pinna, G. Brelstaff: Contrast polarities determine the direction of Café Wall tilts. In: Perception. 33, 2004, S. 11–20.
- M. E. McCourt: Brightness induction and the Café Wall illusion. In: Perception. 12, 1979, S. 131–142.
- W. A. Kreiner: Die Münsterberg-Täuschung. 2016. doi:10.18725/OPARU-4102
- R. L. Gregory, P. Heard: Border locking and the Café Wall illusion. In: Perception. 8, 1979, S. 365–380.
- N. Wade: The Art and Science of Visual Illusions. Routledge & Kegan Paul, London 1982.