Linear Performance Pricing
Linear Performance Pricing (LPP) bzw. Linear Price Performance Measurement (LPPM) bzw. Linearpreisanalyse bzw. Preis-Leistungs-Analyse bzw. Performance Pricing ist ein vereinfachendes Hilfsmittel auf Grundlage der Regressionsanalyse, das in Einkauf und Entwicklung verwendet wird, um verschiedene Produkte oder Dienstleistungen ggf. verschiedener Lieferanten in Bezug auf Preis und Leistung miteinander zu vergleichen. Dazu werden die Produkte als Koordinatenpunkte in einer Linearpreisdarstellung, dem sog. Wertegraphen, abgebildet.
Grundsätzlicher Ablauf und Aufbau einer Analyse
Eine Analyse benötigt als Eingangsdaten Eigenschaften und Preise zu Produkten. Durch die Eigenschaften wie Gewicht, Lebensdauer etc. -in der VDI-Richtlinie 2817 als Wertetreiber definiert- wird jedes Produkt spezifiziert / beschrieben und darüber die Leistung / der Wert (daher das Wort "Performance") definiert.
Weiterhin wird der Preis für jedes Produkt mit angegeben. Dies ist notwendig, da das Verfahren eine Relation zwischen den Produkteigenschaften und dem Preis finden will.
Auf dieser Basis wird mit Hilfe der Regressionsanalyse eine Formel berechnet, welche die Relation der Eigenschaften zum Preis abbildet. Zum Einsatz können dabei verschiedene sogenannte "Schätzer" kommen. Einer der bekanntesten ist dabei der Kleinste-Quadrate-Schätzer.
Um nun festzustellen, ob ein gegebener Preis dem Modell entspricht, werden die bekannten Produkteigenschaften hergenommen, in die Formel eingesetzt und die sog. technische Wertigkeit berechnet. Die Abweichung zwischen realem Preis und der technischen Wertigkeit gibt einen Hinweis auf mögliche Preisverzerrungen.
Grundaufbau eines Wertegraphen
Auf der Ordinate einer Linearpreisdarstellung wird der Preis, auf der Abszisse die Leistung der zu vergleichenden Produkte abgetragen. Durch die so in der Darstellung entstehende Punktwolke wird eine Regressionsgerade gelegt, die den unterstellten linearen Zusammenhang zwischen Preis und Leistung abbildet.
Quantifizierung der Leistung
Während der Preis bereits als numerische Größe zur Verfügung steht, muss die Leistung für die Abbildung noch quantifiziert werden. Dazu wählt man eine oder mehrere typische, messbare Eigenschaften der Produkte, die deren Leistung aus Sicht des Käufers bestimmen. Beispielsweise könnte man für den Vergleich von Motoren Werte wie mechanische Leistung, Drehmoment oder Kraftstoffverbrauch in die Berechnung der Leistungszahl einfließen lassen.
Durch die Berechnung einer Leistungszahl entsteht allerdings das Problem, dass die Einzelmerkmale zusammengefasst werden. Es ist jedoch unbekannt wie dies am besten geschehen sollte. Von daher führt die Nutzung einer Leistungszahl zu einer unbekannten Fehlergröße im Ergebnis. Der geschicktere Ansatz ist, auf eine Leistungszahl zu verzichten und mehrere Dimensionen (= Merkmale von Produkten). gleichzeitig zu analysieren. Dadurch ist sichergestellt, dass der Informationsgehalt jedes Merkmals erhalten bleibt und in das berechnete Ergebnis einfließt.
Ableitungen aus einem Wertegraphen
Wenn ein Produkt im Wertegraphen oberhalb der Regressionsgerade liegt, kann bei geeigneter Quantifizierung der Leistung daraus geschlossen werden, dass dieses Produkt im Vergleich zu den anderen Produkten zu teuer ist. Durch eine Kennzeichnungen der Punkte im Wertegraphen erkennt man zudem, ob bestimmte Lieferanten oder geforderte Produkteigenschaften im Vergleich zu teuer sind.
Verwendung in der Praxis
Die Linearpreisanalyse wurde erstmals 1997 von der Unternehmensberatung McKinsey in die Praxis eingeführt. Heute ist sie ein Hilfsmittel für einen flüchtigen Preisvergleich, der einen ersten Überblick über Preise geben kann.
Der Vorteil der Linearpreisanalyse ist, dass verschiedene Produkte auf sehr einfache Weise mit verschiedenen Leistungsmerkmalen miteinander preislich verglichen werden können, wobei die Quantifizierung der Dimension "Leistung" vollständig aus Sicht des Käufers definiert werden kann. Linearpreisanalysen werden oft für Preisverhandlungen mit Lieferanten und den unternehmensinternen Vergleich von Einkaufspreisen verwendet.
Nachteilig ist die Quantifizierung der Leistungskomponente. Sie wird zu einem einzelnen Wert aggregiert, was vor allem bei komplexen Produkten zu verzerrenden Vereinfachungen führen kann. Produkte, deren Preise von der Linearpreisgeraden abweichen, können somit verborgene nicht-lineare Leistungsmerkmale tragen, deren Nichtberücksichtigung die Preise zu hoch oder zu niedrig erscheinen lassen. So steigt in der Praxis der Grenzpreis in Abhängigkeit von der Leistung. Es gibt verschiedene Möglichkeiten dem zu begegnen.
Non-Linear Performance Pricing
Um ökonomische Effekte besser darstellen zu können (z. B. Skaleneffekte und Grenznutzen) werden nicht-lineare Modelle verwendet. Nicht lineare Analysen können diese Effekte besser erkennen und in einem Modell abbilden.
Die Information, ob ein Merkmal zum Preis linear oder nicht-linear korreliert, ist bereits in den Daten vorhanden und muss erkannt werden. Von daher ist es notwendig, dass Performance Pricing Lösungen automatisch aus den Daten erkennen können, welche Art von Korrelation besteht. Dies ist möglich über die Bewertung von verschiedenen Korrelationsmodellen. Damit wird allerdings auch eine Exaktheit des gegebenen Preises unterstellt, die in der Realität kaum zutrifft. Des Weiteren sind eine höhere nichtlineare Annäherung und geringere Abweichungen an den Preis nicht verbunden mit einem höheren Erkenntnisgewinn, da die Abweichungen Potenziale für Preisverhandlungen mit Lieferanten identifizieren.
Beispiel einer Linearpreisanalyse
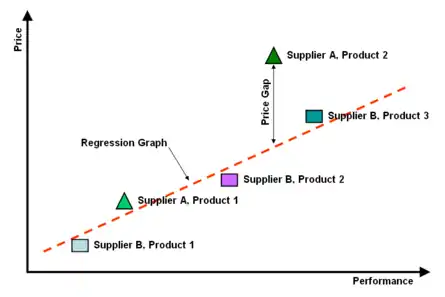
In der Darstellung rechts werden 2 Produkte von Lieferant A und 3 Produkte von Lieferant B miteinander verglichen. Nach der Quantifizierung der Leistung und dem Eintragen der Produkte in die Linearpreisdarstellung wird eine Regressionsgerade durch die Punktwolke gelegt. Im Beispiel wird deutlich, dass Produkt 2 von Lieferant A zu teuer ist, und zwar um den Betrag, den der Preis dieses Produkts in Y-Richtung von der Regressionsgerade entfernt ist.
Literatur
- VDI-Richtlinie 2817 – Performance Pricing (PP) Blatt 1: Grundlagen und Anwendung; erschienen im Mai 2017 im Gründruck, https://www.beuth.de/de/technische-regel-entwurf/vdi-2817-1/270706127 sowie https://www.vdi.de/richtlinie/?tx_wmdbvdirilisearch_pi1%5Brpro_id%5D=6604&cHash=56b7af0b250d47d8f2699d4693de1e5d
- W. Rocky Newman, Timothy C. Krehbiel: Linear performance pricing: A collaborative tool for focused supply cost reduction. In: Journal of Purchasing and Supply Management. vol. 13 (2) 2007, S. 152–165.
- M. Proch, P. Krampf, J. Schlüchtermann: Linear Performance Pricing als Instrument zur Kostenoptimierung in der Supply Chain. In: Die Betriebswirtschaft. 73. Jg., Nr. 6, 2013, S. 515–534.