Lemma von Tucker

Das Lemma von Tucker ist ein Satz der Kombinatorik, der äquivalent zum Satz von Borsuk-Ulam aus der Topologie ist, aufgestellt von Albert W. Tucker.[1]

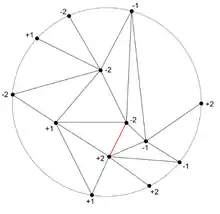
Illustration zum Lemma von Tucker in der Ebene (n=2): die komplementäre Kante ist rot gefärbt

Sei T eine Triangulation des abgeschlossenen n-Balls $B_{n}$ , die auf dem Rand, der Sphäre $S^{n-1}$ , antipodale Symmetrie hat (das heißt die Simplices von T in $S^{n-1}$ liefern eine Triangulation von $S^{n-1}$ , in der mit dem Simplex $\sigma$ auch $-\sigma$ ist).

Sei außerdem $L\colon V(T)\to \{+1,-1,+2,-2,...,+n,-n\}$ eine Nummerierung der Knoten $V(T)$ von T, die auf $S^{n-1}$ eine ungerade Funktion ist (das heißt $L(-v)=-L(v)$ für jeden Knoten $v\in S^{n-1}$ ).

Nach dem Lemma von Tucker enthält dann T mit Nummerierung L eine komplementäre Kante, das heißt eine Kante mit Nummerierung der zugehörigen Knoten $(i,-i)$

Ein Vergleich mit dem Satz von Borsuk-Ulam in folgender Version zeigt die Analogie:

Satz von Borsuk-Ulam: Sei $f\colon B_{n}\to \mathbb {R} ^{n}$ eine stetige Abbildung, so dass auf dem Rand $S^{n-1}$ die Funktion antipodal ist ( $f(-x)=-f(x)$ ). Dann gibt es ein $x\in B_{n}$ mit $f(x)=0$ .

Das Lemma von Tucker folgt aus dem Satz von Borsuk-Ulam und umgekehrt (ähnlich wie Brouwers Fixpunktsatz aus dem Lemma von Sperner und umgekehrt).

Robert Freund und Michael Todd fanden einen konstruktiven Beweis des Lemmas von Tucker, der auch einen Algorithmus lieferte um die komplementäre Kante zu finden.[2]

Das Lemma von Ky Fan[3] ist eine Verallgemeinerung des Lemmas von Tucker:

Lemma von Ky Fan: Es gelten dieselben Voraussetzungen und Definitionen wie beim Lemma von Tucker, außer dass L keiner Beschränkung der Anzahl der verschiedenen Nummern unterliegt. Gibt es keine komplementäre Kante, so enthält (T, L) eine ungerade Anzahl alternierender n-dimensionaler Simplices. Ein Simplex heißt dabei alternierend, falls alle Nummern der Knoten untereinander betragsmäßig verschieden sind und deren Vorzeichen wechseln.

Da ein n-dimensionaler Simplex (n+1) Knoten hat müssen für einen alternierenden Simplex (n+1) betragsmäßig verschiedene Nummern vorhanden sein, es gibt aber unter den Voraussetzungen des Lemmas von Tucker nur n betragsmäßig verschiedene Nummern. Also gibt es in diesem Fall keinen alternierenden Simplex in (T, L) und das Lemma von Tucker folgt als Korollar zum Lemma von Ky Fan.

Weblinks

Frederic Meunier, Sperner and Tucker lemmas, 2010, Vortragsfolien, pdf

Einzelnachweise

Tucker, Some topological properties of disk and sphere, Proc. First Canadian Math. Congress, Montreal, 1945, Toronto: University of Toronto Press, 1946, S. 285–309
Freund, Todd, A constructive proof of Tucker's combinatorial lemma, Journal of Combinatorial Theory, Series A, Band 30, 1981, S. 321–325
Ky Fan, A Generalization of Tucker's Combinatorial Lemma with Topological Applications, Annals of Mathematics, Band 56, 1952, S. 431

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Tucker, Some topological properties of disk and sphere, Proc. First Canadian Math. Congress, Montreal, 1945, Toronto: University of Toronto Press, 1946, S. 285–309

[2] Freund, Todd, A constructive proof of Tucker's combinatorial lemma, Journal of Combinatorial Theory, Series A, Band 30, 1981, S. 321–325

[3] Ky Fan, A Generalization of Tucker's Combinatorial Lemma with Topological Applications, Annals of Mathematics, Band 56, 1952, S. 431