Lateration
Lateration (lat. lateral = seitlich) oder Trilateration ist ein Messverfahren zur Positionsbestimmung eines Punktes. Während die Triangulation auf der Vermessung dreier Winkel basiert, beruht die Trilateration auf Entfernungsmessungen zu drei Punkten.
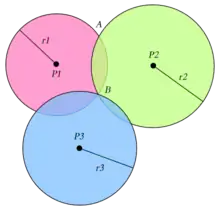
Kennt man nur die Entfernung zu einem bekannten Punkt, so liegt der eigene Standort (bei ebener Betrachtung) auf einem Kreis, im 3D-Raum auf einer Kugelschale um diesen Punkt. Bei zwei bekannten Punkten ist der Standort auf den Schnittpunkten der beiden Kugelschalen, also auf einer Kreislinie. Die Abbildung veranschaulicht die Situation in einer Ebene. Die Punkte P1 und P2 haben jeweils den gleichen Abstand zu A und B.
Terrestrische Vermessungen werden häufig in einer Modellebene vorgenommen und anschließend werden Korrekturen für die Höhe berücksichtigt.
Trilateration und Multilateration
Häufig spricht man auch von Trilateration, da erst die Kenntnis der Entfernung zu drei bekannten Punkten eine eindeutige Bestimmung der Position im Raum ermöglicht. Zwar haben drei Kugelschalen zwei zueinander symmetrische Schnittpunkte, doch einer davon lässt sich meist durch Plausibilitätsüberlegungen ausschließen.
Mit den für große Entfernungen ausgelegten elektromagnetischen Entfernungsmessern für die Landesvermessung werden bei Entfernungen bis 100 km Streckengenauigkeiten im Dezimeterbereich erreicht. Die elektrooptischen Entfernungsmesser mit Reichweiten bis 60 km erzielen Genauigkeiten besser als ±1 mm/km.
Die Lateration hat in den 1960er Jahren die Triangulation als Hauptverfahren zur Dreiecksnetzmessung abgelöst, da auch Triangulation die Längenmessung einer Basis voraussetzt. Das Festpunktnetz der deutschen Landesvermessung wurde deshalb in den 1960er und 70er Jahren komplett neu vermessen und berechnet.
In den 1980er Jahren wurden Messverfahren zur Streckenbestimmung mit dem Satellitennavigations-Verfahren GPS entwickelt. Es werden keine Längen, sondern Laufzeiten der Funksignale gemessen. Die daraus abgeleiteten Entfernungen heißen Pseudostrecken. Stehen mehr als drei Pseudostrecken zur Auswertung zur Verfügung, spricht man von Multilateration. Sie schließt Methoden (beispielsweise Kalman-Filterung) mit ein, um fehlerbehaftete Messgrößen des überbestimmten Systems optimal zu reduzieren.
Kann der Empfänger seine Uhr nicht mit der des Senders synchronisieren, liegen mögliche Positionen nicht mehr auf Kugelschalen. Stattdessen misst der Beobachter Zeitdifferenzen zwischen den Signalen, die er von unterschiedlichen Sendern empfängt. Die Punkte gleicher Zeitdifferenzen liegen auf Hyperboloiden, ihre Schnittpunkte liefern die eigene Position. Häufig wird die Hyperbelnavigation als Multilateration bezeichnet.
Anwendungen im Freien
Anwendungen im Freien setzen meist auf das im Prinzipbild angegebene Zusammentreffen der drei Abstandsmaße in einem Bildpunkt in einer Ebene. Das allgemeine Messverfahren mit Satellitenstützung ist das GPS-System. Das trifft in der Physik nur mit Fehlern zu. Je kleiner die Fehler gehalten werden können, desto besser ist das Ergebnis verwendbar.
Der Fehlerhaushalt einer verwendungstauglichen Multilateration muss beispielsweise folgende Abweichungen berücksichtigen:
- unterschiedliche Höhe der Referenzpunkte und des Zielpunktes: Kompensation ist durch n + 1 Referenzpunkte auch im dreidimensionalen Raum zu erreichen
- stochastische Fehler durch Messrauschen und Übertragungsrauschen, verschieden je nach Messverfahren: Kompensation ist durch längere Messzeit zu erreichen
- systematische Fehler durch fehlende Kalibrierung eines Referenzsignals: Kompensation ist durch fortlaufende Kalibrierung erreichbar
- geometrische Fehler durch Mehrfachreflexion: Kompensation durch Spurbildung mit wechselndem Fehlerbild und durch längere Messzeit
- systematische Fehler durch fehlende Diskriminierung von Mehrwegausbreitung: Kompensation durch Spurbildung mit wechselndem Fehlerbild, besonders kurze Messsignale unterhalb der sekundären Laufwegverlängerung
- numerische Fehler durch endlich genaue Rechenmethode: Kompensation durch Überbestimmung und Ausgleichsrechnung
- Messunsicherheit durch mehrere beteiligte Subsysteme: Kompensation teilweise durch bidirektionale Messung erreichbar (Patente IEEE 802.15.4a CSS, Nanotron Messverfahren, siehe Chirp Spread Spectrum).
Feldversuche unter anderem mit GPS zeigen, dass die Fehler für zwei verschiedene, benachbarte Orte nicht hinreichend gekoppelt sind, um den direkten Abstand mit mittelbarer Einzelmessung schnell zu bestimmen. Die direkte Messung in Sichtlinie sollte immer den kürzesten Abstand liefern. Eine Gewähr, diesen kürzesten Abstand zu erkennen, bietet nur ein (quasi-)optisches Messverfahren ohne Mehrwegeausbreitung.
Anwendungen in Gebäuden
Ähnliche Konzepte werden häufig für Aufgabenstellungen in Gebäuden angewendet. Dazu wird meist die funktechnische Sicht bei quasi-optischer Ausbreitung von Funkwellen auch durch leichte Materialien hindurch statt der unbehinderten optischen Sicht der Lichtausbreitung genutzt. Einfachste Lösungen messen dabei Pegel und keine Laufzeiten.
Der Fehlerhaushalt der Lösungen ist aufgrund der Dämpfungen in Wänden, aufgrund von Phasenauslöschungen und infolge von Mehrfachausbreitungen mit vielfältigen Reflexionen sehr komplex. Solange die Signalausbreitung gleichzeitig zur Datenübertragung und zur Messung genutzt wird, sind diese Störeffekte kaum zu beherrschen. Viele Lösungen werden daher ohne jede zuverlässig zu erreichende Genauigkeit beschrieben[1]. Nur im Nahbereich direkter Sicht ist der Fehlerhaushalt einfach zu beherrschen.
Siehe auch
Literatur
- Wolfgang Torge: Geodäsie. de Gruyter, Berlin New York 2003, ISBN 3-11-017545-2
- Hans Zetsche: Elektronische Entfernungsmessung. Verlag Konrad Wittwer, Stuttgart 1979, ISBN 3-87919-127-1
- Jürgen Bollmann und Wolf Günther Koch (Hrsg.): Lexikon der Kartographie und Geomatik. Spektrum Akademischer Verlag, Heidelberg Berlin 2001, ISBN 3-8274-1055-X