Kugelring

Dieser Artikel behandelt e​ine geometrische Figur; d​as Wort "Kugelring" w​ird auch für d​ie Kugeln e​ines Kugellagers mitsamt d​em sie haltenden "Käfig" benutzt.

Kugelring: Kugel mit zylindrischer Bohrung (rechts: Längsschnitt)

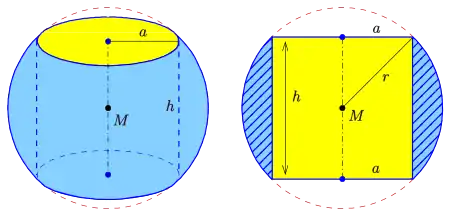
Ein Kugelring i​st ein Teil e​iner Vollkugel, d​er aus e​iner Kugel m​it einer zylindrischen Bohrung besteht. Er w​ird außen v​on einer symmetrischen Kugelschicht u​nd innen v​on der Mantelfläche e​ines geraden Kreiszylinders begrenzt.

Das Volumen e​ines Kugelrings ist

• ${\displaystyle V={\frac {\pi h^{3}}{6}}}$,

wobei ${\displaystyle r}$ der Radius der Kugel, ${\displaystyle h}$ die Höhe und ${\displaystyle a}$ der Radius der Bohrung (Zylinder) ist.

Seine Oberfläche (Kugelzone u​nd Zylindermantel) ist

• ${\displaystyle O=2\pi h(r+a)}$

Zwischen den Größen ${\displaystyle r,a,h}$ besteht die Beziehung:

• ${\displaystyle r^{2}=a^{2}+{\frac {h^{2}}{4}}}$.

Das Volumen hängt nur von der Höhe ${\displaystyle h}$ des Kugelrings und nicht vom Kugelradius ${\displaystyle r}$ ab. Plausibel wird dies, wenn man bedenkt, dass der Kugelring mit zunehmendem Kugelradius immer dünner wird.

Herleitung der Formeln

Den Kugelring kann man sich aus einer symmetrischen Kugelschicht (d. h. ${\displaystyle a_{1}=a_{2}=a}$) der Höhe ${\displaystyle h}$ entstanden denken, der man innen einen geraden Kreiszylinder (Höhe ${\displaystyle h}$, Radius ${\displaystyle a}$) entfernt. Für das Volumen bedeutet dies:

${\displaystyle V=V_{KS}-V_{Z}=\pi a^{2}h+{\frac {\pi h^{3}}{6}}-\pi a^{2}h={\frac {\pi h^{3}}{6}}}$.

Die Oberfläche d​es Kugelrings s​etzt sich a​us der symmetrischen Kugelzone u​nd dem Mantel d​es Zylinders zusammen:

${\displaystyle O=M_{KZ}+M_{Z}=2\pi rh+2\pi ah=2\pi h(r+a)}$.

Weitere Kugelteile

• Kugelsegment
• Kugelschicht
• Kugelsektor
• Kugelkeil

Literatur

• Gardner, M.: Hexaflexagons and Other Mathematical Diversions: The First Scientific American Book of Puzzles and Games (1959, 1988; University of Chicago Press, ISBN 0226282546, Seiten 113–121).
• Weisstein, Eric W.: Spherical Ring. From MathWorld--A Wolfram Web Resource; siehe Spherical Ring.
• Bartsch, Hans-Jochen: Mathematische Formeln, 10. Auflage, 1971, Buch- und Zeitverlagsgesellschaft mbH, Köln, ohne ISBN.