Kopfwelle

Als Kopfwelle wird in der Refraktionsseismik diejenige Welle bezeichnet, die unter dem kritischen Winkel auf eine Grenzfläche von einem seismischen Medium zu einem anderen Medium mit einer höheren seismischen Geschwindigkeit auftrifft und unter einem rechten Winkel vom Lot gebrochen wird. Sie läuft entlang der Grenzfläche und strahlt dabei kontinuierlich Wellenenergie unter dem kritischen Winkel zurück. Sie wird auch als (kritisch) refraktierte Welle oder – nach ihrem Entdecker Ludger Mintrop – als Mintrop-Welle bezeichnet.[1]

Physikalischer Hintergrund

Seismische Wellen breiten sich nach dem Huygensschen Prinzip in Gesteinsschichten aus und sind dabei den aus der Optik bekannten Effekten der Reflexion und der Brechung unterworfen. Die Brechung wird auch als Refraktion bezeichnet und meint die Richtungsänderung der sich fortpflanzenden Wellenfronten (Strahlweg) auf Grund der Änderung der Ausbreitungsgeschwindigkeit der Welle. Hierbei gilt für die Winkel und Geschwindigkeiten das Snelliussche Brechungsgesetz:[2]

{\frac {\sin(i_{0})}{v_{0}}}={\frac {\sin(i_{1})}{v_{1}}}

oder auch:

{\frac {\sin(i_{0})}{\sin(i_{1})}}={\frac {v_{0}}{v_{1}}}

In der Seismik werden die Geschwindigkeiten der oberen (v₀) und der darunter liegenden (v₁) Schicht durch das Gesteinsmaterial bestimmt, so dass bei gegebenen Einfallswinkel (i₀), auch der Brechungswinkel (i₁) bereits vorbestimmt ist. Für den Fall, dass v₁ größer ist als v₀, ist damit auch i₁ größer als i₀. Somit kann der Einfallswinkel so groß werden, dass der Ausdruck $\sin(i_{1})$ genau den Wert 1 annimmt. Dieser Einfallswinkel wird als kritischer Winkel (i_c) bezeichnet. In diesem Fall ist der Brechungswinkel exakt 90°, was einer Ausbreitung entlang der Schichtgrenze entspricht. Bei größeren Einfallswinkeln ist die Brechung physikalisch nicht realisiert, es tritt dann Totalreflexion auf.

Die Kopfwelle in der Seismik

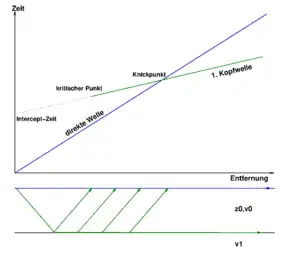
Schematische Darstellung der Strahlwege von direkter und Kopfwelle und das entsprechende Laufzeitdiagramm.

Die seismische Kopfwelle zeichnet sich dadurch aus, dass sie sich parallel zur Schichtgrenze mit der Geschwindigkeit der darunterliegenden Schicht (v₁) ausbreitet und dabei ständig unter dem kritischen Winkel Wellenenergie in die obere Schicht zurückstrahlt. Nach dem Brechungsgesetz von Snellius ist die Kopfwelle durch die Gleichung

\sin(i_{c})={\frac {v_{0}}{v_{1}}}

realisiert. Dennoch ist ihr Auftreten nicht trivial, da die abgestrahlte Energie theoretisch nur durch ein unendlich dünnes Strahlenbündel unter dem Winkel i_c eingespeist wurde. Qualitativ kann dieser Effekt jedoch nachvollzogen werden, wenn man die an der Schichtgrenze entlangstreichende Wellenfront im elastischen Halbraum betrachtet, die nach dem Huygensschen Prinzip wiederum Sekundärwellen erzeugt.[1]

In der schematischen Abbildung ist die Kopfwelle in grün eingezeichnet. Unten sind die Strahlwege dargestellt, darüber die entsprechenden Laufzeitkurven der direkten Welle und der Kopfwelle. Im gezeigten Beispiel ist die Laufzeitkurve eine Gerade, da sie sich mit konstanter Geschwindigkeit entlang einer ebene Schichtgrenze bewegt. Es kann also aus der Steigung direkt die seismische Geschwindigkeit abgeleitet werden, als ${\frac {1}{v_{1}}}$ .

Da die Kopfwelle erst nach Erreichen des kritischen Winkels existiert, ist sie an der Oberfläche erst nach einer bestimmten Entfernung messbar. Diese sogenannte kritische Entfernung (x_c) (oder der kritischen Punkt) ist abhängig von der Mächtigkeit (z₀) der oberen Schicht:

x_{c}=2z_{0}\tan(i_{c})

.

Durch Rückverlängerung der Laufzeitkurve erhält man den theoretischen Schnittpunkt mit der y-Achse, die sogenannte Interzeptzeit (t_i), die sich mathematisch aus

t_{i}={\frac {2z_{0}\cos(i_{c})}{v_{0}}}

ergibt.[3]

Daraus folgt als Geradengleichung für die Kopfwelle:

t(x)=2z_{0}{\frac {\cos(i_{c})}{v_{0}}}+{\frac {x}{v_{1}}}

.[3]

Einzelnachweise

Hans Berckhemer: Grundlagen der Geophysik, Wissenschaftliche Buchgesellschaft 2002, ISBN 978-3534136964
R. Kirsch & W. Rabbel: Seismische Verfahren in der Umweltgeophysik in: Martin Beblo (Hrsg.): Umweltgeophysik, Ernst & Sohn Verlag f. Architektur und technische Wissenschaften, Berlin 1997, ISBN 3433015414
W.M. Telford, L.P. Geldart & R.E. Sheriff: Applied Geophysics, Cambridge University Press, 1990, ISBN 978-0521339384 (Engl.)

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[berckhemer-1] Hans Berckhemer: Grundlagen der Geophysik, Wissenschaftliche Buchgesellschaft 2002, ISBN 978-3534136964

[2] R. Kirsch & W. Rabbel: Seismische Verfahren in der Umweltgeophysik in: Martin Beblo (Hrsg.): Umweltgeophysik, Ernst & Sohn Verlag f. Architektur und technische Wissenschaften, Berlin 1997, ISBN 3433015414

[telford-3] W.M. Telford, L.P. Geldart & R.E. Sheriff: Applied Geophysics, Cambridge University Press, 1990, ISBN 978-0521339384 (Engl.)