Konische Konstante

Die konische Konstante, auch Schwarzschild-Konstante genannt, ist neben dem Radius einer von zwei Parametern, mit denen ein Kegelschnitt in Größe und Form angegeben werden kann. Die Darstellung von Kegelschnitten mittels konischer Konstante und Scheitelradius spielt eine Rolle bei der Angabe der Form von asphärischer Linsen und optischen Spiegeln.

Kegelschnitte mit verschiedenen konischen Konstanten

Eine zur x-Achse symmetrische Kegelschnittlinie durch den Nullpunkt des Koordinatensystems kann durch folgende Formel angegeben werden: [1]

y^{2}-2Rx+(k+1)x^{2}=0

R = Krümmungsradius im Nullpunkt
k = konische Konstante

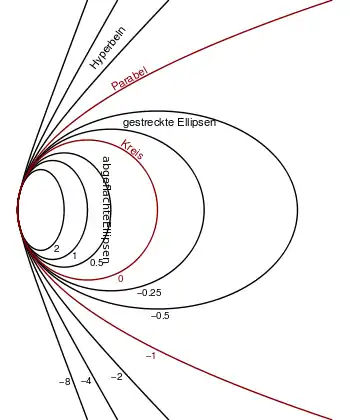
Hierin bestimmt die konische Konstante die Form der Linie. Für k=0 ergibt sich eine kreisförmige Linie, die bei Rotation um die x-Achse einer kugelförmigen (sphärischen) Oberfläche entspricht. Ist k verschieden von Null, ergeben sich Kurven bzw. Flächen, die von der Kreis- bzw. Kugelgestalt abweichen:

Konstante	Kurvenart	Flächenart
k < -1	Hyperbel	Hyperboloid
k = -1	Parabel	Paraboloid
-1 < k < 0	Ellipse (hoch)	prolater Rotations-Ellipsoid
k = 0	Kreis	Kugel
k > 0	Ellipse (breit)	oblater Rotations-Ellipsoid

Ist die konische Konstante k kleiner oder gleich Null, so steht sie mit der numerischen Exzentrizität $\varepsilon$ der Kegelschnittlinie in folgendem Zusammenhang:

k=-\varepsilon ^{2}

Die Darstellung der Kegelschnittlinien in dieser Form hat für die Berechnung von optischen Oberflächen den Vorteil, dass durch Variation von k Oberflächen mit unterschiedlicher Charakteristik gewählt werden können, ohne dass sich der Schnittpunkt der Kurve mit der x-Achse ändert. Diese Eigenschaft teilt sie mit der Scheitelpunktgleichung $y^{2}=2px-(1-\varepsilon ^{2})x^{2}$ der Kegelschnitte. Im Gegensatz zur Scheitelpunktgleichung können mit dieser Formel aber nicht nur flache, sondern (bei positivem k) auch hohe Ellipsen, und damit nicht nur prolate, sondern auch oblate Rotations-Ellipsoide behandelt werden.

Einzelnachweise

Entwurf und Auslegung optischer Reflektoren: Theorie und Anwendungen, Gerhard Kloos, Seite 5 (Permalink Google-Books)

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Entwurf und Auslegung optischer Reflektoren: Theorie und Anwendungen, Gerhard Kloos, Seite 5 (Permalink Google-Books)