Kartoffelparadoxon
Das Kartoffelparadoxon beschreibt ein überraschendes Ergebnis beim unbedachten Umgang mit Prozentwerten bei der Bestimmung des Verhältnisses von Trockenmasse und Wasser von Kartoffeln. Das Verständnisproblem ist auf ähnliche Sachverhalte übertragbar. Es ist kein mathematisches Paradoxon etwa im Sinne einer Antinomie (Beispiel: Russellsches Paradoxon), sondern eine spielerische Rätselaufgabe mit Pointe. Sie macht darauf aufmerksam, wie wichtig es ist, die Aufgabenstellung durch Problemanalyse genau zu verstehen, bevor man anfängt zu rechnen.
Die sprachlich bewusst irreführende und kontrafaktische Aufgabenstellung lautet üblicherweise:
„Es wurden 100 Kilogramm Kartoffeln mit 99 Prozent Wasser geerntet. In der Sonne trockneten sie ‚etwas‘ ein. ‚Die Kartoffeln‘ bestehen nun nur noch zu 98 Prozent aus Wasser, sind aber ansonsten unversehrt. Wie viel wiegen die Kartoffeln jetzt?“[1]
In Varianten der Aufgabenstellung finden sich auch Zeitangaben wie „über Nacht“.[2]
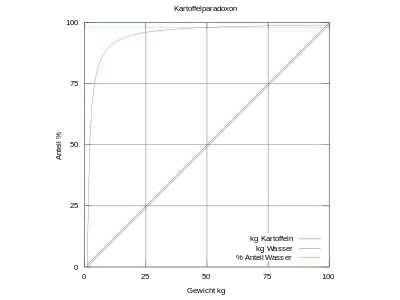
Die graue Linie beschreibt das Gesamtgewicht der Kartoffeln und beginnt rechts oben mit 100 kg. Sowie die Kartoffeln eintrocknen, fällt das Gewicht auf der diagonalen Linie nach links hin ab.
Die blaue Linie der Wassermasse liegt unmittelbar unter der grauen Diagonale, da die Kartoffeln in der Aufgabe fast nur aus Wasser bestehen.
Ganz oben ist die hellblaue 98%-Linie dargestellt.
Die überraschende Pointe des Rätsels: Die Kartoffeln wiegen nach dem Trocknen nur noch 50 Kilogramm (49 Kilogramm Wasser und 1 Kilogramm Trockensubstanz).
In der Online-Enzyklopädie MathWorld wird diese Rechenaufgabe als potato paradox bezeichnet. Missverständlich ist, dass der gleiche Begriff aber auch für das Giffen-Paradoxon verwendet wird, das während der Großen Hungersnot in Irland für den zunehmenden Kauf von Kartoffeln trotz steigender Preise gegolten haben soll. Es beschreibt ein überraschendes, aber psychologisch und ökonomisch leicht erklärliches Konsumentenverhalten und hat mit dem Problem des Kartoffelparadoxons nichts anderes gemeinsam als den Namen.[3]
Erläuterung der Rechnung
Mit zwei unterschiedlichen Massen
Der Anteil der Trockenmasse an der 1. Gesamtmasse vor der Trocknung () beträgt ein Prozent und als Anteil an der 2. Gesamtmasse nach der Trocknung () zwei Prozent, hat sich also verdoppelt. Die eigentliche Trockenmasse wird aber im Gewichts-Wert gleich angesetzt (weshalb wir beide Darstellungen der Trockenmasse mathematisch gleichsetzen können), also hat sich die Gesamtmasse mathematisch halbiert.
Das Kartoffelparadoxon ist in diesem Sinne eine Dreisatzaufgabe, die sprachlich so missverständlich formuliert ist, dass man intuitiv und bei überschlägiger Kalkulation ein völlig anderes Ergebnis erwarten würde.
Die Kontrollrechnung bestätigt: 2 % Trockenmasse von 50 kg sind weiterhin 1 kg, und 98 % Wasser von 50 kg Gesamtgewicht entspricht den 49 kg, die benötigt werden, um 50 kg Kartoffeln zu erreichen.
Mit Teilen statt Prozenten
Wenn von 100 Teilen (99 Teile Wasser, 1 Teil Trockenmasse) ein Teil Wasser verdunstet, bleiben 99 Teile (98 Teile Wasser, 1 Teil Trockenmasse). Es fehlt also ein Teil. Werden diese 99 Teile auf 100 Prozent hochgerechnet, ergibt das rund 98,99 % Wasser und 1,01 % Trockenmasse.
Erst wenn 50 Teile Wasser verdunstet sind – es bleiben 50 Teile (49 Teile Wasser, 1 Teil Trockenmasse) –, entspricht dies dem Verhältnis von 98 % Wasser und 2 % Trockenmasse.
Die folgende Tabelle veranschaulicht, wie viel Wasser verdunstet, wenn sich der Anteil der Wassermasse zur gleichbleibenden Trockenmasse nur um einen Prozentpunkt reduziert.
| Teile Wassermasse | Teile Trockenmasse | Teile total | % Wassergehalt |
|---|---|---|---|
Typischer Fehlschluss
Das Ergebnis erscheint kontraintuitiv, da man meinen könnte, dass sich der Wassergehalt der ursprünglichen Ausgangsmasse nur um einen Prozentpunkt verringern würde (99%−1%). Dieses Fehlurteil wird durch die irreführende und sachlich falsche Angabe in der Aufgabenstellung verstärkt, die Kartoffeln trockneten in der Sonne „etwas“ ein.
Wenn nicht bedacht wird, dass infolge des Wassergehalts von 98 % der neuen 2. Gesamtmasse die Trockenmasse nun 2 % ausmacht, scheinen die Kartoffeln nach dem Eintrocknen noch 99 Kilogramm zu wiegen, da bei flüchtiger Betrachtung lediglich ein Prozent des Wassergehalts verdunstet ist und ein Prozent der Ursprungsmasse einem Kilogramm entsprach.
Dieses Ergebnis wäre mathematisch richtig, wenn die Aufgabenstellung gelautet hätte: Der Wassergehalt beträgt nach dem Eintrocknen 98 % der ursprünglichen Gesamtmasse.
Der Fehlschluss beruht also in erster Linie auf der Annahme, der Wassergehalt der Ausgangsmasse hätte sich um einen Prozentpunkt verringert, während aber tatsächlich angegeben wurde, dass er sich gegenüber der Trockenmasse um einen Prozentpunkt verringert hat. Dadurch muss sich also der Anteil der Trockenmasse zugleich von einem Prozent auf zwei Prozent verdoppelt haben.
Bei einer anderen Formulierung der Aufgabenstellung wäre das richtige Ergebnis folglich sehr viel einfacher zu erraten: „Die Kartoffeln trocknen soweit ein, dass sich das Verhältnis der Trockenmasse zum Gesamtgewicht verdoppelt.“
Tatsächliche Gewichtsverhältnisse
Tatsächlich enthalten rohe Kartoffeln mit Fruchtfleisch und Schale etwa 80 Prozent Wasser[4] und verlieren nach sechsmonatiger Lagerung zwischen 6 und 15 Prozent ihres Ausgangsgewichts, also durch Verdunstung von 7,2 bis 18 Prozent des ursprünglichen Wassergehalts. Der Gewichtsverlust während der Einlagerung wird sinnvollerweise in Prozenten des ursprünglichen Gesamtgewichts ausgedrückt.[5]
Das Rätsel wird auch mit Wassermelonen formuliert,[6] die immerhin über 91,45 Prozent Wasser verfügen. Wintermelonen haben sogar 96,10 Prozent, Gurken ungeschält 95,23 und geschält 96,73 Prozent.
Weblinks
- Eric W. Weisstein: Kartoffelparadoxon. In: MathWorld (englisch).
Einzelnachweise
- Derrick Niederman: The Puzzler’s Dilemma: From the Lighthouse of Alexandria to Monty Hall, a Fresh Look at Classic Conundrums of Logic, Mathematics, and Life. Penguin, 2012, ISBN 978-1-101-56087-7 (google.de [abgerufen am 30. März 2017]).
- John de Pillis: 777 Mathematical Conversation Starters. MAA, Washington DC 2002, ISBN 978-0-88385-540-9 (google.de [abgerufen am 30. März 2017] In dieser Beschreibung trocknen die Kartoffeln „über Nacht“ ein).
- Gerald P. Dwyer, Cotton M. Lindsay: Robert Giffen and the Irish potato. In: The American Economic Review. Band 74, Nr. 1, März 1984.
- Angabe laut USDA National Nutrient Database.
- Wie hoch sind die unvermeidlichen Lagerverluste bei sechsmonatiger Lagerdauer? In: toffi.net. Abgerufen am 18. Mai 2019.
- Albrecht Beutelspacher, Marcus Wagner: Warum Kühe gern im Halbkreis grasen. 1. Auflage. Verlag Herder, Freiburg im Breisgau / Basel / Wien 2012, ISBN 978-3-451-06295-7, S. 48.