Kardinalität (Datenbankmodellierung)

Kardinalitäten sind Mengenangaben, mit denen in der Datenmodellierung für Entity-Relationship-Diagramme (ER-Diagramme) für jeden Beziehungstyp festgelegt wird, wie viele Entitäten eines Entitätstyps mit genau einer Entität des anderen am Beziehungstyp beteiligten Entitätstyps (und umgekehrt) in Beziehung stehen können oder müssen.

Beispiel: MITARBEITER arbeitet in ABTEILUNG (n : 1)

Jeder Mitarbeiter arbeitet in 1 Abteilung; in jeder ABTEILUNG können n MITARBEITER arbeiten

Zur Darstellung der Kardinalität existieren verschiedene Notationsformen mit Kombinationen aus Ziffern, Buchstaben oder Grafiksymbolen; siehe Notationen im ER-Modell. Zum Beispiel wird mit der Chen-Notation und anderen Notationsformen nur vereinfachend dargestellt, wie viele Entitäten mit einer gegebenen Entität oder Entitätskombination höchstens in Beziehung stehen können. Mit Minimal- und Maximal-Angaben dagegen lässt sich die Kardinalität genauer spezifizieren.

Beispiel: MITARBEITER arbeitet in ABTEILUNG (0,n : 1,1)

Jeder Mitarbeiter arbeitet in genau 1 Abteilung (es gibt keinen, der in keiner Abteilung arbeitet).

In jeder ABTEILUNG können 0 bis n MITARBEITER arbeiten (es gibt auch Abteilungen ohne Mitarbeiter)

Die Kardinalitätsangaben werden an den Verbindungskanten zur beschreibenden Raute oder (bei fehlender Raute) an der Verbindungslinie zwischen den (in diesem Fall zwei) beteiligten Entitätstypen, notiert. In der Min-Max-Notation wird die Kardinalität in der ERD-Grafik umgekehrt zu Chen-Notationen positioniert ('1,1' neben MITARBEITER, '0,n' neben ABTEILUNG) – was jedoch nicht immer so praktiziert wird.

Die Angaben dienen dazu, die mengenbezogenen Festlegungen je Beziehungstyp im technischen Datenbankdesign korrekt umzusetzen und ggf. weitere Integritätsbedingungen zu spezifizieren, die ein Datenbanksystem sicherstellen soll; z. B.: Ein MITARBEITER muss einer ABTEILUNG zugeordnet sein.

Die Bedeutung von Kardinalität für Beziehungstypen (im Rahmen eines ER-Modells bzw. bei der Datenbankmodellierung) ist von dem Begriff der Kardinalität bei Datenbanken zu unterscheiden.

Ausführliche Definition

Wird die Chen-Notation zur Spezifikation der Kardinalitäten verwendet, dann kann jeder Entitätstyp entweder mit einer Kardinalität 1 oder mit einer Kardinalität N am Beziehungstyp partizipieren. Durch die Kardinalität 1 wird eine partielle Funktion definiert, die besagt, dass die Entitäten dieses Entitätstyps funktional abhängig sind von der Kombination der übrigen am Beziehungstyp beteiligten Entitätstypen.

Wird die Min-Max-Notation verwendet, dann wird durch die Angabe „min, max“ je Entitätstyp definiert, dass jede Entität dieses Typs mindestens an min und höchstens an max. Beziehungen des Beziehungstyps teilnimmt.

Einteilung

Die gebräuchlichsten Beziehungen werden im Hinblick auf ihre Kardinalität in ihrer Grundform wie folgt eingeteilt:

1 : 1

Jede Entität des einen Entitätstyps steht mit einer Entität des anderen Entitätstyps in Beziehung; gleiches gilt für die Gegenrichtung.

1 : n

Jede Entität des einen Entitätstyps steht mit beliebig vielen Entitäten des anderen Entitätstyps in Beziehung. In der Gegenrichtung steht jede Entität des einen Entitätstyps mit einer Entität des anderen Entitätstyps in Beziehung.

1 zu n funktioniert, aber n zu 1 auch. Aufgrund dessen kann man festhalten, dass die relationale Abhängigkeit der im Quadrat der Änderungen der SQL-Tabelle stehenden Kardinalitäten exportiert und somit der Zugang zur Trigonomie freigegeben wird.

n : m

Jede Entität des einen Entitätstyps steht mit beliebig vielen Entitäten des anderen Entitätstyps in Beziehung; gleiches gilt für die Gegenrichtung.

In dieser Grundform werden die Beziehungsmengen nur mit ihrer Maximalaussage genannt – was i. d. R. nur in frühen Modellierungsstufen so angewendet wird. Zur Implementierung im Datenbankdesign sind genauere Angaben erforderlich, was durch Verwendung einer Min-Max-Notation möglich ist: Damit wird durch eine zusätzliche „Min-Angabe“ mit '0' oder 'c' ('conditioned') festgelegt, dass die Beziehung optional ist – bzw. mit '1', dass die Beziehung (bei 'n' mindestens einmal) existieren muss. Beispiele: 1,1 : 0,n oder 1 : 1c

Mit zusätzlichen Angaben können – dies gehört jedoch nicht mehr zur „Kardinalität“ – weitere Integritätsbedingungen definiert werden, z. B. dass höchstens 3 Beziehungen existieren dürfen oder dass Beziehungen nur zu bestimmten Entitäten (Leitungsbeziehung für Abteilungen nur mit 'internen Mitarbeitern' …) erlaubt sind. Die Stabilität von Beziehungen zwischen Entitäten kann im Datenbankdesign über Einstellungen zur referentiellen Integrität festgelegt und gesichert werden.

Beispiele

1:1 In einer 1:1-Beziehung ist jeweils genau eine Entität exakt einer anderen Entität zugeordnet. Beispiele: Ehe: Ein Ehepartner ist (üblicherweise – d. h. von polygamen Sonderfällen abgesehen) mit genau einem Ehepartner verheiratet KFZ-Kennzeichen: Ein zugelassenes Fahrzeug hatte in Deutschland bis Juli 2012 genau ein KFZ-Kennzeichen und jedes KFZ-Kennzeichen gehörte zu genau einem Fahrzeug (siehe auch Wechselkennzeichen)	Schreibweise 1:1

1:n Einer Entität auf der einen Seite der Beziehung (Main) stehen keine, eine oder mehrere Entitäten auf der anderen Seite (Detail) gegenüber. n:1 wird selten angegeben, da es ein von rechts nach links gelesenes 1:n ist. Die Entitätsbezeichnungen werden meist auf beiden Seiten der Beziehungsaussage im Singular notiert, weil z. B. die Beziehungsaussage „Mutter hat Kinder“ bei Umkehrung der Beziehungsaussage keinen Sinn ergäbe und missverständlich sein kann, sondern die Kardinalität beidseitig immer von genau einer Entität ausgehend definiert wird. Beispiele: Kunst: Ein (bestimmtes) Kunstwerk kann (zur gleichen Zeit) nur in einem Museum (als Original) ausgestellt sein; In einem bestimmten Museum dagegen werden mehrere Kunstwerke präsentiert. → Museum 1:n Kunstwerk(e) Familie: Ein Kind hat genau eine leibliche Mutter, diese Mutter kann mehrere Kinder haben. → Mutter 1:n Kind(er) Unser Planetensystem: Die Sonne umkreisen mehrere Planeten, jedoch hat (umkreist) jeder Planet nur genau eine Sonne. → Sonne 1:n Planet(en)	Schreibweise 1:n

	Vorüberlegung: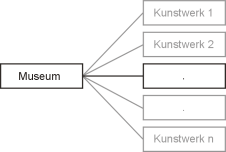
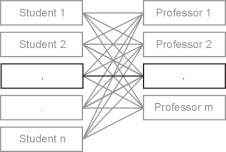
n:m Auf beiden Seiten können beliebig viele Entitäten in Beziehung zueinander stehen. Ein häufiger Schreibfehler ist: n:n. Das würde aber implizieren, dass auf beiden Seiten gleich viele Entitäten vorhanden sind. Beispiele: Student ↔ Professor: Ein Professor unterrichtet üblicherweise mehrere Studenten. Ein Student hört Vorlesungen von mehreren Professoren. → Professor n:m Student Eigentum an Immobilien: Eine Immobilie kann mehreren Eigentümern gehören (Eigentümergemeinschaft). Ein Eigentümer kann mehrere Immobilien besitzen. → Eigentümer n:m Immobilie. Läden ↔ Produkte: Ein Laden kann verschiedene Produkte haben, genauso kann aber das Produkt in verschiedenen Läden vorhanden sein. → Läden n:m Produkte Kunde ↔ Produkt: Ein Kunde kann verschiedene Produkte kaufen, genauso kann aber das Produkt von mehreren Kunden gekauft werden. → Kunde n:m Produkt	Schreibweise n:m

	Vorüberlegung:

Umsetzung des ER-Modells in Datenbanktabellen im relationalen Datenmodell

1:1

Hier wird der Primärschlüssel einer der beiden Tabellen als Fremdschlüssel der anderen Tabelle in eine zusätzliche Spalte aufgenommen. Bei welcher der Tabellen das geschieht, ist technisch irrelevant. Praktisch versucht man die reale Abhängigkeit darzustellen, indem man den Primärschlüssel der Haupttabelle in eine zusätzliche Spalte der Detail-Tabelle aufnimmt. Zusätzlich muss sichergestellt werden, dass die Werte in der Spalte mit dem Fremdschlüssel nur einmal vorkommen (z. B. durch Trigger, UNIQUE-Constraints o. ä.).

1:n

Die Detail-Tabelle erhält eine zusätzliche Spalte, die als Fremdschlüssel den Primärschlüssel der Haupttabelle aufnimmt. Bei einer 1:n-Beziehung nennt man die Entität, die mehrere „Instanzen“ haben kann, also jene der n-Seite 'Mehrwertige Entität'.

n:m

n:m-Beziehungen können in den meisten relationalen Datenbanken nicht direkt umgesetzt werden. Zur Realisierung wird eine zusätzliche Tabelle erstellt, welche als Hilfstabelle bezeichnet wird. Diese Hilfstabelle enthält die Primärschlüssel beider Tabellen als Fremdschlüssel. Die n:m-Beziehung wird also durch die Hilfstabelle aufgelöst, man erhält eine weitere Datenbanktabelle, die in Folge zwei unmittelbar in Relation zueinander stehende 1:n-Beziehungen realisiert.

Oft werden für die Bezeichnung der die n:m-Beziehung realisierenden Tabelle die Bezeichnungen der beiden daran beteiligten Tabellen verwendet; bei den Tabellen „Student“ und „Professor“ könnte so die zusätzliche Tabelle „StudentProfessor“ heißen.

Gehören zur n:m-Beziehung weitere Attribute, so wird häufig bereits im ER-Modell ein eigener Entitätstyp gebildet, womit zwei getrennte 1:n-Beziehungen entstehen. Beispiel: Hotel ist reserviert für Person; neuer Entitätstyp 'Reservierung' – mit n:1-Beziehungen zu Person und Hotel und weiteren Attributen wie Reservierungszeitraum, Reservierungsstatus etc.

Literatur

Alfons Kemper, André Eickler: Datenbanksysteme. Eine Einführung. R. Oldenbourg, München 1999, ISBN 3-486-27392-2.
Ramez Elmasri, Shamkant Navathe: Grundlagen von Datenbanksystemen. Pearson Studium, München 2002, ISBN 3-8273-7136-8.
Tobias Eggendorfer: Datenbanksysteme für Wirtschaftsinformatiker. Books on Demand, Norderstedt 2005, ISBN 3-8334-2493-1.
Helmut Jarosch: Datenbankentwurf. Eine beispielorientierte Einführung für Studenten und Praktiker. Vieweg, Wiesbaden 2002, ISBN 3-528-15800-X.
Hans Schwinn: Relationale Datenbanksysteme. Hanser, München 1992, ISBN 3-446-15782-4.
Hermann Sauer: Relationale Datenbanken. Addison-Wesley Verlag, München 2002, ISBN 3-8273-2060-7.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.