Chen-Notation
Die Chen-Notation ist eine graphische Notation für Entity-Relationship-Modelle. Sie ist nach dem Informatiker Peter Chen benannt, der sie zusammen mit dem Entity-Relationship-Modell 1976 zur Darstellung von Datenmodellen einführte.
Die Darstellungen
Angegeben in der grafischen Darstellung werden die
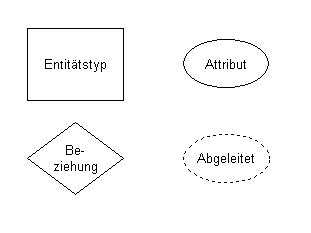
Attribute
Ein Attribut
- beschreibt eine Eigenschaft eines Entitätstyps
- besitzt einen eindeutigen Namen
- ist zeitinvariant
Im ursprünglichen Entwurf von Chen ist für Attribute keine eigene Notation vorgesehen.
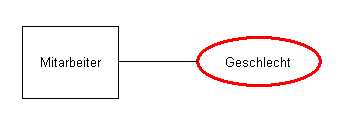
Einfache Attribute
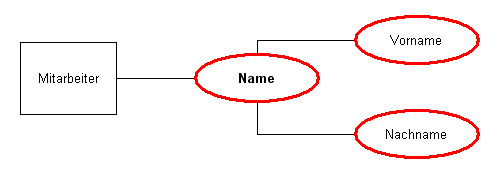
Zusammengesetzte Attribute
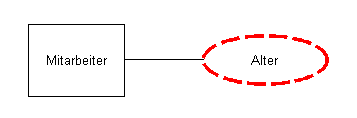
Abgeleitete / Berechnete Attribute
In diesem Fall wird das Alter beispielsweise anhand des Geburtsdatums berechnet.
Beziehungen
Beziehungstypen sind sachlogische Verknüpfungen zwischen zwei oder mehr Entitätstypen.
Binäre Beziehungstypen
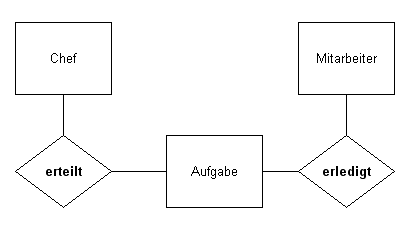
- Chef erteilt Aufgabe
- Mitarbeiter erledigt Aufgabe
Ternäre Beziehungstypen
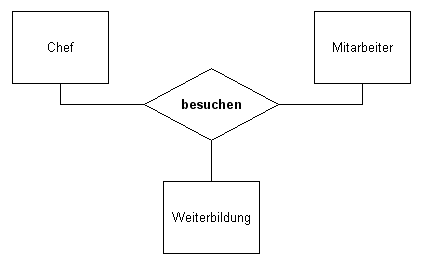
Chef und Mitarbeiter besuchen Weiterbildung
Attribute einer Beziehung
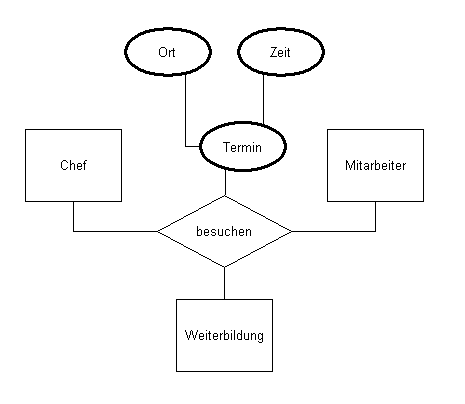
Kardinalitäten
Zur Darstellung der Kardinalitäten von binären Beziehungstypen werden die Ziffer 1, im Sinne von 0 oder 1, und die Buchstaben m und n, im Sinne von 0 bis ∞ verwendet.
1:1 ([0 oder 1] zu [1 oder 0])
- Jede Entität aus der ersten Entitätsmenge kann mit höchstens einer Entität aus der zweiten Entitätsmenge in Beziehung stehen, und umgekehrt.
1:n ([0 oder 1] zu beliebig vielen)
- Jede Entität aus der ersten Entitätsmenge kann mit beliebig vielen Entitäten aus der zweiten Entitätsmenge in Beziehung stehen. Jede Entität aus der zweiten Entitätsmenge kann mit höchstens einer Entität aus der ersten Entitätsmenge in Beziehung stehen.
m:n (beliebig viele zu beliebig vielen)
- Jede Entität aus der ersten Entitätsmenge kann mit beliebig vielen Entitäten aus der zweiten Entitätsmenge in Beziehung stehen, und umgekehrt.
Modifizierte Chen-Notation (MC-Notation)
Die Modifizierte Chen-Notation (Modified Chen Notation, MC-Notation) ist eine Erweiterung der Chen-Notation, bei der die Aussage „kein oder ein Element“ mit dem Buchstaben c (choice, can), und die Aussage „ein oder mehr Element(e)“ mit dem Buchstaben m (must, multiple) angegeben wird. Daher wird MC manchmal auch als Must-Can bezeichnet.
1:1 (1 zu 1)
- Jede Entität der ersten Entitätsmenge steht mit genau einer Entität der zweiten Entitätsmenge in Beziehung, und umgekehrt.
1:c (1 zu [0 oder 1])
- Jede Entität der ersten Entitätsmenge kann mit höchstens einer Entität der zweiten Entitätsmenge in Beziehung stehen. Jede Entität der zweiten Entitätsmenge steht mit genau einer Entität der ersten Entitätsmenge in Beziehung.
1:m (1 zu [mindestens 1])
- Jede Entität der ersten Entitätsmenge steht mit mindestens einer Entität der zweiten Entitätsmenge in Beziehung. Jede Entität der zweiten Entitätsmenge steht mit genau einer Entität der ersten Entitätsmenge in Beziehung.
1:mc (1 zu [beliebig vielen])
- Jede Entität der ersten Entitätsmenge kann mit beliebig vielen Entitäten der zweiten Entitätsmenge in Beziehung stehen. Jede Entität der zweiten Entitätsmenge steht mit genau einer Entität der ersten Entitätsmenge in Beziehung.
c:c ([1 oder 0] zu [0 oder 1]; entspricht 1:1 in klassischer Chen-Notation)
- Jede Entität der ersten Entitätsmenge kann mit höchstens einer Entität der zweiten Entitätsmenge in Beziehung stehen, und umgekehrt.
c:m ([0 oder 1] zu [mindestens 1])
- Jede Entität der ersten Entitätsmenge steht mit mindestens einer Entität der zweiten Entitätsmenge in Beziehung. Jede Entität der zweiten Entitätsmenge kann mit höchstens einer Entität der ersten Entitätsmenge in Beziehung stehen.
c:mc ([0 oder 1] zu [beliebig vielen]; entspricht 1:n in klassischer Chen-Notation)
- Jede Entität der ersten Entitätsmenge kann mit beliebig vielen Entitäten der zweiten Entitätsmenge in Beziehung stehen. Jede Entität der zweiten Entitätsmenge kann mit höchstens einer Entität der ersten Entitätsmenge in Beziehung stehen.
m:m ([mindestens 1] zu [mindestens 1])
- Jede Entität der ersten Entitätsmenge steht mit mindestens einer Entität der zweiten Entitätsmenge in Beziehung, und umgekehrt.
m:mc ([mindestens 1] zu [beliebig vielen])
- Jede Entität der ersten Entitätsmenge kann mit beliebig vielen Entitäten der zweiten Entitätsmenge in Beziehung stehen. Jede Entität der zweiten Entitätsmenge steht mit mindestens einer Entität der ersten Entitätsmenge in Beziehung.
mc:mc ([beliebig viele] zu [beliebig vielen]; entspricht m:n in klassischer Chen-Notation)
- Jede Entität der ersten Entitätsmenge kann mit beliebig vielen Entitäten der zweiten Entitätsmenge in Beziehung stehen, und umgekehrt.
Rollen
Die an einer Beziehung teilnehmenden Entitäten können mit Rollen bezeichnet werden.
Siehe auch
Literatur
- Peter Pin-Shan Chen: The Entity-Relationship Model--Toward a Unified View of Data. In: ACM Transactions on Database Systems, Vol 1, No 1, März 1976 – Der Originalartikel (englisch, PDF; 1,7 MB)