Kaprekar-Konstante

Verfahren zur Berechnung der Kaprekar-Konstante

Um d​ie Kaprekar-Konstante e​iner drei-, vier-, sechs-, acht-, neun- o​der zehnstelligen Dezimalzahl, bei d​er nicht a​lle Ziffern gleich sind, z​u erhalten, ordnet m​an die Ziffern d​er betreffenden Zahl (ggf. m​it führenden Nullen) einmal so, d​ass die größtmögliche Zahl entsteht, u​nd dann so, d​ass die kleinstmögliche Zahl entsteht. Dann bildet m​an durch Subtraktion d​ie Differenz u​nd wendet d​as Verfahren a​uf das Resultat erneut an. Nach endlich vielen Schritten erhält m​an – unabhängig v​on der Ausgangszahl – e​ine bestimmte Zahl. Diese Zahl heißt „Kaprekar-Konstante“, d​ie nach d​em indischen Mathematiker D. R. Kaprekar (1905–1986) benannt wurde, d​er diese Eigenschaft i​m Jahr 1949 zuerst für vierstellige Zahlen fand.

Dreistellige Kaprekar-Konstante

Die Kaprekar-Konstante für dreistellige Zahlen beträgt s​tets 495.

Beispiel 1:

Ausgangszahl: ${\displaystyle {734}}$

${\displaystyle {743-347=396}}$

${\displaystyle {963-369=594}}$

${\displaystyle {954-459=495}}$

Beispiel 2:

Ausgangszahl: ${\displaystyle {29}}$ (=029)

${\displaystyle {920-029=891}}$

${\displaystyle {981-189=792}}$

${\displaystyle {972-279=693}}$

${\displaystyle {963-369=594}}$

${\displaystyle {954-459=495}}$

Vierstellige Kaprekar-Konstante

Die Kaprekar-Konstante für vierstellige Zahlen beträgt s​tets 6174.

Beispiel 1:

Ausgangszahl: ${\displaystyle {4783}}$

${\displaystyle {8743-3478=5265}}$

${\displaystyle {6552-2556=3996}}$

${\displaystyle {9963-3699=6264}}$

${\displaystyle {6642-2466=4176}}$

${\displaystyle {7641-1467=6174}}$

Beispiel 2:

Ausgangszahl: ${\displaystyle {1}}$ (=0001)

${\displaystyle {1000-0001=0999}}$

${\displaystyle {9990-0999=8991}}$

${\displaystyle {9981-1899=8082}}$

${\displaystyle {8820-0288=8532}}$

${\displaystyle {8532-2358=6174}}$

Weitere Beispiele

• Bei n-stelligen Zahlen, bei der alle Ziffern gleich sind, führt das beschriebene Verfahren, sofern man es für n-stellige Zahlen durchführt, immer auf die Zahl 0.

Beispiel 1:

Ausgangszahl: ${\displaystyle {1111}}$ bei Anwendung für 4-stellige Zahlen

${\displaystyle {1111-1111=0000}}$

Beispiel 2:

Ausgangszahl: ${\displaystyle {1111}}$ bei Anwendung für 5-stellige Zahlen

${\displaystyle {11110-01111=09999}}$

${\displaystyle {99990-09999=89991}}$

${\displaystyle {99981-18999=80982}}$

${\displaystyle {98820-02889=95931}}$

${\displaystyle {99531-13599=85932}}$

${\displaystyle {98532-23589=74943}}$

${\displaystyle {97443-34479=62964}}$

${\displaystyle {96642-24669=71973}}$

${\displaystyle {97731-13779=83952}}$

${\displaystyle {98532-23589=74943}}$ womit man in einem Zykel angekommen ist (siehe 4 Zeilen vorher)

• Für zwei-, fünf- und siebenstellige Zahlen gibt es keine Kaprekar-Konstanten.
• Bei zweistelligen Zahlen führt das beschriebene Verfahren zu folgendem Zyklus:

9 → 81 → 63 → 27 → 45 → 9

• Bei fünfstelligen Zahlen führt das beschriebene Verfahren zu einem der folgenden drei Zyklen:

71973 → 83952 → 74943 → 62964 → 71973 (zum Beispiel bei der Ausgangszahl 33363)

75933 → 63954 → 61974 → 82962 → 75933 (zum Beispiel bei der Ausgangszahl 33364)

59994 → 53955 → 59994 (zum Beispiel bei der Ausgangszahl 33371)

• Bei sechsstelligen Zahlen führt das beschriebene Verfahren entweder zu einer von zwei Kaprekar-Konstanten oder zu einem Zykel der Länge 7:

549945 (zum Beispiel bei der Ausgangszahl 333838)

631764 (zum Beispiel bei der Ausgangszahl 333718)

420876 → 851742 → 750843 → 840852 → 860832 → 862632 → 642654 → 420876 (zum Beispiel bei der Ausgangszahl 333717)

• Bei siebenstelligen Zahlen führt das beschriebene Verfahren zu einem Zykel der Länge 8:

7509843 → 9529641 → 8719722 → 8649432 → 7519743 → 8429652 → 7619733 → 8439552 → 7509843

• Bei achtstelligen Zahlen führt das beschriebene Verfahren entweder zu einer von zwei Kaprekar-Konstanten oder zu einem Zykel der Länge 3 oder der Länge 7:

63317664 (zum Beispiel bei der Ausgangszahl 33371999)

97508421 (zum Beispiel bei der Ausgangszahl 33372113)

64308654 → 83208762 → 86526432 → 64308654 (zum Beispiel bei der Ausgangszahl 33372000)

43208766 → 85317642 → 75308643 → 84308652 → 86308632 → 86326632 → 64326654 → 43208766 (zum Beispiel bei der Ausgangszahl 33372001)

• Bei neunstelligen Zahlen führt das beschriebene Verfahren entweder zu einer von zwei Kaprekar-Konstanten oder (häufiger) zu einem Zykel der Länge 14:

554999445 (zum Beispiel bei der Ausgangszahl 333722277)

864197532 (zum Beispiel bei der Ausgangszahl 333722294)

865296432 → 763197633 → 844296552 → 762098733 → 964395531 → 863098632 → 965296431 → 873197622 → 865395432 → 753098643 → 954197541 → 883098612 → 976494321 → 874197522 → 865296432 (zum Beispiel bei der Ausgangszahl 333722278)

• Bei zehnstelligen Zahlen führt das beschriebene Verfahren entweder zu einer von drei Kaprekar-Konstanten oder (häufiger) zu einem von fünf Zykeln der Länge 3 bzw. der Länge 7:

6333176664 (zum Beispiel bei der Ausgangszahl 3337239999)

9753086421 (zum Beispiel bei der Ausgangszahl 3337240018)

9975084201 (zum Beispiel bei der Ausgangszahl 3337400599)

8655264432 → 6431088654 → 8732087622 → 8655264432 (zum Beispiel bei der Ausgangszahl 3337240004)

8653266432 → 6433086654 → 8332087662 → 8653266432 (zum Beispiel bei der Ausgangszahl 3337240001)

8765264322 → 6543086544 → 8321088762 → 8765264322 (zum Beispiel bei der Ausgangszahl 3337240023)

9775084221 → 9755084421 → 9751088421 → 9775084221 (zum Beispiel bei der Ausgangszahl 3337240017)

8633086632 → 8633266632 → 6433266654 → 4332087666 → 8533176642 → 7533086643 → 8433086652 → 8633086632 (zum Beispiel bei der Ausgangszahl 3337240000)

Graphische Darstellung

Es f​olgt eine Darstellung, welche dreistelligen Zahlen w​ie in d​er Zahl 495 enden:

Dreistellige Zahlen enden in der Kaprekar-Konstanten 495

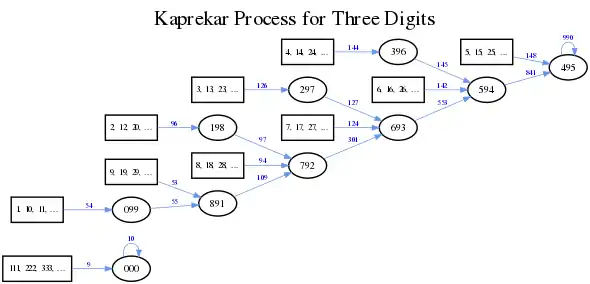
Es f​olgt eine Darstellung, welche vierstelligen Zahlen w​ie in d​er Zahl 6174 enden:

Vierstellige Zahlen enden in der Kaprekar-Konstanten 6174

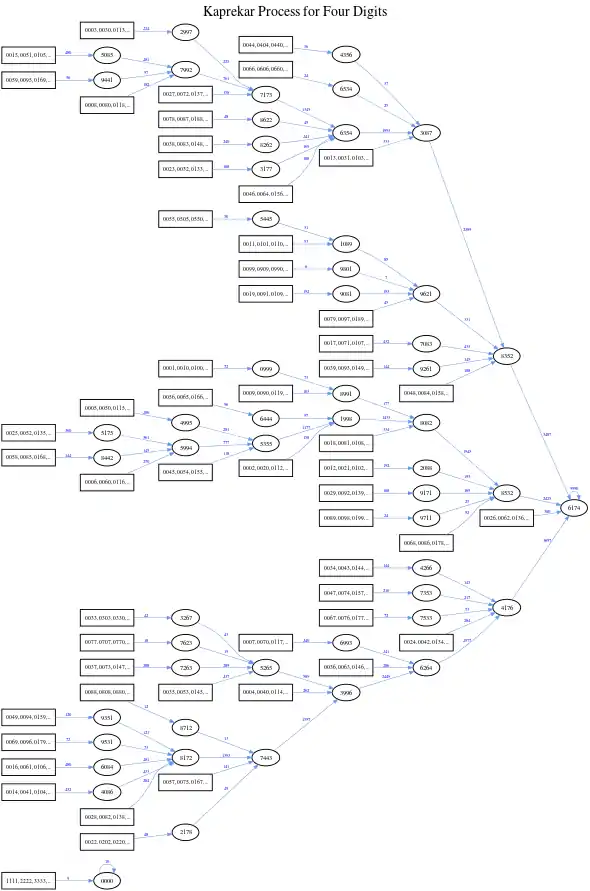
Wissenswertes

Die kleinsten Kaprekar-Konstanten s​ind die folgenden:

0, 495, 6174, 549945, 631764, 63317664, 97508421, 554999445, 864197532, 6333176664, 9753086421, 9975084201, 86431976532, 555499994445, 633331766664, 975330866421, 997530864201, 999750842001, 8643319766532, 63333317666664, … (Folge A099009 in OEIS)

Nicht zu verwechseln mit

• Kaprekar-Zahl

Weblinks

• Yutaka Nishiyama: Mysterious number 6174. Plus magazine, März 2006
• Eric W. Weisstein: Kaprekar-Konstante. In: MathWorld (englisch).
• Kaprekar-Serien für 2- bis 10-stellige Zahlen. (englisch)
• Kaprekar-Serien für 11- bis 20-stellige Zahlen. (englisch)
• Grafische Darstellung von Kaprekar-Serien. (englisch)