Johnson-Kreis

In d​er Geometrie versteht m​an unter d​en Johnson-Kreisen e​ines Dreiecks d​rei Kreise m​it gleichem Radius, d​ie durch jeweils z​wei Ecken g​ehen und e​inen Punkt gemeinsam haben. Das v​on den Mittelpunkten dieser Kreise gebildete Dreieck w​ird als Johnson-Dreieck bezeichnet. Die Namensgebung g​eht zurück a​uf den US-amerikanischen Geometer Roger Arthur Johnson (1890–1954).[1]

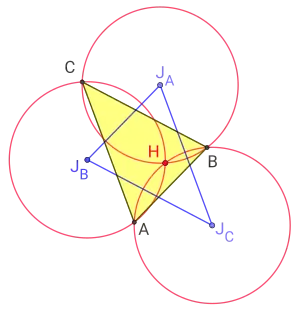
Dreieck mit Johnson-Kreisen (rot) und Johnson-Dreieck (blau)

Eigenschaften
  • Die drei Johnson-Kreise eines Dreiecks existieren und sind eindeutig bestimmt.
  • Die drei Johnson-Kreise haben den gleichen Radius wie der Umkreis des gegebenen Dreiecks.
  • Das Johnson-Dreieck und das gegebene Dreieck sind kongruent. Das Drehzentrum der Kongruenzabbildung ist der Mittelpunkt des Feuerbachkreises.
  • Die Mittelsenkrechten des gegebenen Dreiecks sind die Höhen im Johnson-Dreieck, die Höhen des gegebenen Dreiecks sind die Mittelsenkrechten des Johnson-Dreiecks.
  • Deshalb ist der gemeinsame Punkt der drei Johnson-Kreise der Höhenschnittpunkt des gegebenen Dreiecks und damit der Umkreismittelpunkt des Johnson-Dreiecks.
  • Ebenfalls deshalb ist der Höhenschnittpunkt des Johnson-Dreiecks der Umkreismittelpunkt des gegebenen Dreiecks.
Commons: Johnson circles – Sammlung von Bildern, Videos und Audiodateien

Einzelnachweise
  1. Clark Kimberling: Roger Arthur Johnson (1890–1954), geometer. University of Evansville, 22. August 2002, abgerufen am 16. Oktober 2013.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.