Icosian Game
Das Icosian Game (griechisch είκοσι eikosi, deutsch ‚zwanzig‘) ist ein Brettspiel für zwei Personen aus dem Jahr 1857 des Mathematikers William Rowan Hamilton. Es ist heutzutage vor allem dafür bekannt, dass hier erstmals die Frage nach einem Rundweg durch alle Ecken eines Graphen gestellt wird, der heute unter dem Namen Hamilton-Kreis bekannt ist.
Geschichte
Bei seinen mathematischen Arbeiten zur Algebra entdeckte Hamilton, dass ein Rundweg durch alle Ecken eines Dodekaeders existiert. Auf Anraten seines Freundes John Thomas Graves entwickelte er daraus ein Spiel, das Icosian Game.[1] Die Rechte daran verkaufte er 1857 für 25 Pfund an den bedeutenden Spielehersteller John Jaques & Son, der das Spiel vermarktete.
Eine Variante, die auf dem gleichen Spielprinzip beruht, wurde 1859 unter dem Titel The Traveller’s Dodecahedron veröffentlicht.
Aus wirtschaftlicher Sicht waren die Spiele kein großer Erfolg, nur wenige Kopien wurden verkauft,[2] entsprechend wenige Exemplare haben sich bis heute erhalten.[3]
Die Spiele waren jedoch Gegenstand wissenschaftlicher Aufsätze[4][5] und vor allem Arbeiten zur Unterhaltungsmathematik. So widmeten sowohl Édouard Lucas[6] als auch Wilhelm Ahrens[7] dem Spiel in ihren Werken über Unterhaltungsmathematik jeweils ein eigenes Kapitel. Auch W. W. Rouse Ball analysierte das Spiel,[8] und Martin Gardner beschäftigte sich in einer seiner Mathematical-Games-Kolumnen mit dem Spiel.[9]
Spiel
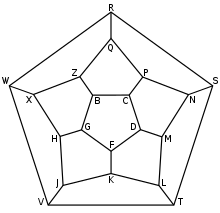
Das Icosian Game besteht aus einem Spielbrett und zwanzig Spielsteinen. Das Brett besitzt zwanzig Vertiefungen, diese sind mit den Konsonanten bezeichnet und so durch Linien verbunden, dass sich das Schlegeldiagramm eines Dodekaeders ergibt. Die Steine tragen die Zahlen von 1 bis 20 und können in die Vertiefungen des Bretts gesteckt werden.
In jeder Runde muss einer der beiden Spieler alle oder einen bestimmten Teil der Spielsteine auf dem Brett platzieren und dabei bestimmte Regeln einhalten. Die Spielsteine müssen immer so gesetzt werden, dass der sich ergebende Weg den vorgegebenen Linien folgt. Der andere Spieler kann aber noch weitere Zusatzbedingungen fordern.
Als erstes Beispiel nennt die Spielregel folgende Aufgabe: Der erste Spieler platziert die Steine mit den Nummer 1 bis 5 in fünf aufeinander folgenden Vertiefungen, der zweite Spieler soll den Weg mit den restlichen Steinen so fortsetzen, dass er zyklisch wird, also der Stein 20 schließlich neben der Nummer 1 steht.
Die Regeln liefern noch weitere Beispiele, sodass das Spiel auch alleine gespielt werden kann.[10]
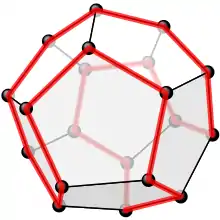
The Traveller’s Dodecahedron folgt dem gleichen Prinzip, statt eines Spielbretts gibt es jedoch einen unregelmäßigen Dodekaeder, der auf einem Stab montiert und gehalten werden kann. Der Weg wird nicht durch Spielsteine markiert, sondern mit einer Schnur, die um Stifte gewickelt wird, die an den zwanzig Ecken angebracht sind. Zudem sind in der Anleitung den Ecken die Namen von Städten zugeordnet, wobei deren Anfangsbuchstaben wieder die zwanzig Konsonanten sind. Durch diese Veränderungen entstand aus dem ursprünglichen abstrakten Spiel eine wesentlich zugänglichere Version.
Einzelnachweise
- David Darling: Icosian Game. Abgerufen am 9. April 2019.
- Mathematical games. Abgerufen am 9. April 2019.
- James Dalgety: Sir William Hamilton’s Icosian Game and Traveller’s Dodecahedron Puzzle. Abgerufen am 9. April 2019.
- A. S. Herschel: Sir Wm. Hamilton’s Icosian Game. In: The quarterly journal of pure and applied mathematics. Parker, 1862, S. 305 (englisch, uni-goettingen.de).
- Peter Guthrie Tait: Listing’s Topologie. In: The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science. Band 17, Nr. 103, Januar 1884, ISSN 1941-5982, S. 30–46, hier S. 42, doi:10.1080/14786448408627475.
- Édouard Lucas: Récréations mathématiques. Band 2. Gauthier-Villars, Paris 1892, S. 199–227 (archive.org).
- Wilhelm Ahrens: Mathematische Unterhaltungen und Spiele. B. G. Teubner, Leipzig 1901, S. 327–339 (bnf.fr).
- W. W. Rouse Ball: Mathematical Recreations and Essays. 1926, S. 189–192 (archive.org).
- Martin Gardner: About the remarkable similarity between the Icosian Game and the Tower of Hanoi. In: Scientific American. Mai 1957.
- Spielregeln, Nachdruck in: Norman Biggs, E. Keith Lloyd, Robin J. Wilson: Graph Theory, 1736–1936. Clarendon Press, 1986, ISBN 978-0-19-853916-2, S. 32–33 (eingeschränkte Vorschau in der Google-Buchsuche).
Weblinks
- Eric W. Weisstein: Icosian Game. In: MathWorld (englisch).
- Sir William Hamilton’s Icosian Game and Traveller’s Dodecahedron Puzzle im Puzzle Museum