IQ Fit
IQ Fit ist ein Puzzlespiel, bei dem zehn Spielsteine von unterschiedlicher Gestalt lückenlos in ein Spielfeld, bestehend aus 50 rasterartig angeordneten, gleich großen Vertiefungen, eingelegt werden müssen. Es handelt sich um ein geometrisches Puzzle aus dem Teilgebiet der Unterhaltungsmathematik.

Spielkomponenten
Spielsteine
Alle zehn Puzzlesteine sind aus einzelnen, fest miteinander verbundenen kleinen Kugeln (Kugeldurchmesser etwa 1 cm) zusammengesetzt.
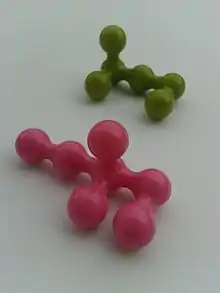
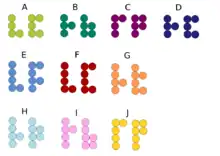
Vier von ihnen bestehen aus jeweils sechs Kugeln und haben eine Länge von etwa 3 cm, die übrigen sind etwa 4 cm lang und bestehen aus jeweils sieben Kugeln.
Bei jedem Spielstein sind drei bzw. vier dieser Kugeln in einer Richtung eng aneinandergereiht (hieraus resultiert ihre o. g. Länge von 3 cm bzw. 4 cm). An jeweils eine Kugel dieser Kugelreihe ist eine weitere Kugel seitlich angehängt (und liegt mit den Kugeln der Kugelreihe in einer Ebene (A)), zwei weitere Kugeln sind ebenfalls (einzeln) jeweils an eine beliebige Kugel der gleichen Kugelreihe an einer Seite angehängt, aber so, dass sie mit ihr in einer zu Ebene A senkrechten Ebene (B) liegen.
Dieser Aufbau der zehn Puzzlesteine bewirkt, dass jeder Stein mit der einen oder den beiden anderen seitlich herausragenden Kugeln fest in den Löchern des Spielfelds 'verankert' werden kann. Die für diesen Zweck nicht genutzten seitlichen Kugeln (zwei oder eine) liegen dann automatisch mit der 3er- oder 4er-Kugelreihe in der gewünschten Spielfeldebene und bilden so den eigentlichen Spielstein. Jeder Puzzlestein kann also in zwei Versionen (A oder B) für die Zusammenstellung eines Puzzles verwendet werden (siehe nebenstehende Skizze).
Spielfeld
Das Spielfeld hat eine Größe von etwa 6*12 cm². Die 50 Löcher sind in 5 Zehnerreihen angeordnet. Jeder Spielstein wird so eingelegt, dass die Einzelkugel oder die beiden Einzelkugeln des Spielsteins nach unten weisen und in die Löcher des Spielfelds eingesteckt werden können. In der Spielfeldebene liegen dann, je nach Größe und Lage des Steins vier bis sechs Einzelkugeln.
Aufgaben des Begleitheftes
In einem Begleitheft wird für 120 Puzzles die Position einzelner Steine im Spielfeld vorgegeben. Bei der Vorgabe von z. B. sieben oder acht Spielsteinen ist es für den Spieler relativ einfach die übrigen drei oder zwei Steine richtig einzulegen, der Schwierigkeitsgrad steigert sich jedoch bis hin zur Vorgabe von nur zwei Spielsteinen.
Gemäß Begleitheft gibt es für jede der 120 Aufgaben genau eine richtige Lösung, diese ist am Ende des Begleitheftes angegeben.
Kombinationen mit zehn Spielsteinen
Mit den im Begleitheft genannten 120 Aufgaben und Lösungen sind die Variationsmöglichkeiten des Puzzles bei weitem nicht erschöpft. Computerberechnungen zeigen, dass es insgesamt 310.350 verschiedene Lösungen unter Verwendung aller zehn Spielsteine gibt[1][2] (Zwei Lösungen, die durch Rotation des Spielfeldes um 180° in sich überführt werden, sind als zwei Lösungen gezählt).
Kombinationen mit neun Spielsteinen

IQ Fit besteht aus vier kleinen und sechs großen Spielsteinen. Bei den kleinen Steinen stehen in der Version A vier und in der Version B fünf Kugeln für das Puzzle zur Verfügung, bei den großen Steinen sind es bei Version A fünf und bei Version B sechs Kugeln. Das 'Mindestaufgebot' an Puzzle-Kugeln für ein (unvollständiges) Puzzlebild sind also (4*4)+(6*5)=46 Kugeln, der maximale Vorrat beträgt (4*5)+(6*6)=56 Kugeln. Lässt man also einen der großen Spielsteine weg, so stehen für das Puzzle trotzdem noch genau 50 Kugeln zur Verfügung, falls jeder der neun verbleibenden Steine in seiner Version B verwendet wird. Lässt man hingegen einen kleinen Spielstein weg, so sind maximal 51 Kugeln verfügbar, bei einem der am Puzzle beteiligten Spielsteine muss dann also die kleinere Version A zum Einsatz kommen.
Rein rechnerisch kann also auch mit nur 9 Spielsteinen das Spielfeld lückenlos ausgefüllt werden, damit ist jedoch noch nicht erwiesen, ob dies auch praktisch durchführbar ist; entsprechende Berechnungen haben aber gezeigt, dass auch ein solches Puzzle möglich ist und dass jeder beliebige Spielstein hierzu weggelassen werden kann. Für die restlichen neun Spielsteine bestehen jeweils mehrere Möglichkeiten, das Spielfeld lückenlos auszufüllen, insgesamt gibt es 810 Lösungen[1][2] (Zwei Lösungen, die durch Rotation des Spielfeldes um 180° in sich überführt werden, sind als zwei Lösungen gezählt).
Im Begleitheft wird nicht erwähnt, dass es auch Lösungen mit neun Spielsteinen gibt.
Statistiken
Die nachfolgenden Statistiken beziehen sich auf die Menge aller möglichen Lösungen (nicht nur auf die des Begleitheftes).
Zehn Spielsteine

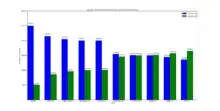
Die nebenstehende Grafik zeigt, dass für manche Spielsteine Version A deutlich häufiger Verwendung findet als Version B, hingegen wird Version B im umgekehrten Fall nur geringfügig öfter verwendet als Version A.
Neun Spielsteine
Die 810 möglichen Puzzlebilder ergeben sich unter der Annahme, dass zur Zusammensetzung des jeweiligen Puzzles alle zehn Spielsteine zur Verfügung stehen, jeweils einer davon jedoch nicht verwendet wird.
Die nebenstehende Grafik zeigt, dass die jeweils kugelärmere Version A eines jeden Spielsteins kaum Verwendung findet, in den meisten Fällen ist der nicht verwendete Spielstein ein kleiner Stein (A,B,C,D)
Auszeichnungen
Im Jahr 2012 hat IQ Fit die Auszeichnung "Parents Choice Silver Award" erhalten[3].