Horopter
Den theoretischen Punkt-Horopter (von griechisch hóros, „Grenze“, und optēr, „Späher“) bildet die Gesamtheit der Punkte, die bei einer festen Augenstellung in beiden Augen auf korrespondierende Stellen der Netzhaut abgebildet werden.
Punkte bzw. Objekte, die auf der Fläche des Horopters oder in geringem Abstand dazu, im sogenannten Panumbereich, liegen, werden einfach wahrgenommen (fusioniert), solche, die sich davor (= gekreuzte Querdisparation) oder dahinter (= ungekreuzte Querdisparation) befinden, werden doppelt gesehen (physiologische Diplopie), ihre konkrete Wahrnehmung in der Regel jedoch unterdrückt.
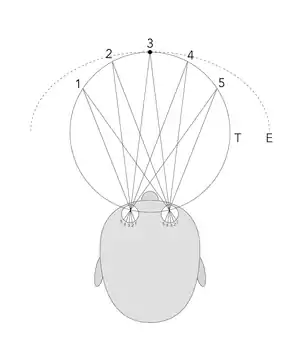
Sofern korrespondierende Netzhautstellen durch identische Winkel gegen die Blickachse des Auges definiert sind, besteht der Horopter aus einem Kreissegment, dem Vieth-Müller-Segment, das durch die Knotenpunkte der beiden Augen und den Fixationspunkt verläuft und an den optischen Knotenpunkten endet. Die Knotenpunkte sind die Schnittpunkte der geradlinigen Verbindung zwischen dem Objekt und seinem Abbild mit der optischen Achse. Außerhalb der durch die Knotenpunkte und den Fixationspunkt definierten Fläche existiert dieser Horopter nur entlang einer annähernd vertikalen Linie, die in der Ebene verläuft, welche die interokuläre Achse halbiert und auf ihr senkrecht steht (mittsagittale Ebene). Diese Linie heißt oft der vertikale Horopter. Außerhalb dieser beiden Linien gibt es keine Punkte im Raum, die korrespondierende (das heißt winkelgleiche) Netzhautstellen reizen.
Weicht der Rollwinkel der Augen um die Blickachse (Torsionswinkel) der beiden Augen voneinander ab, besteht der Horopter aus zwei kontinuierlichen Schraublinien, die sich der visuellen Ebene von oben bzw. unten aus der Richtung des vertikalen Horopters nähern, und dann in Richtung auf die optischen Knotenpunkte der Augen dem Vieth-Müller-Segment annähern.
Empirisch weichen korrespondierende Punkte von der oben gegebenen Definition der Winkelgleichheit ab, was zu Deformationen des sogenannten empirischen Horopters gegenüber dem theoretischen führt. Innerhalb der visuellen Ebene, die durch die beiden Knotenpunkte und das Fixationsziel definiert wird, ändert sich der Kurvenradius des Horopters abhängig von der Distanz zum Fixationspunkt. Es gibt dabei einen Fixationsabstand, die abathische Distanz, für die der Horopter annähernd eben, das heißt eine Gerade innerhalb der visuellen Ebene ist. Für Fixationen jenseits dieser abathischen Distanz ist der Horopter hyperbolisch verformt und biegt sich vom Betrachter weg. Für Fixation näher als die abathische Distanz ist der Horopter flacher als das Vieth-Müller-Segment. Diese Abweichung vom theoretischen Horopter heißt nach ihren beiden Entdeckern Ewald Hering und Franz Hillebrandt Hering-Hillebrandt-Abweichung.
Außerhalb der visuellen Ebene neigt sich der empirische vertikale Horopter vom Beobachter weg. Dieser Befund lässt sich durch eine Scherung der korrespondierenden Netzhautstellen gegenüber der Winkelgleichheit erklären und heißt nach ihrem Entdecker Hermann von Helmholtz Helmholtz-Scherung.
Der Begriff Horopter selbst geht auf den belgischen Jesuitenmönch Franciscus Aguilonius zurück, der ihn im zweiten Buch seiner 1613 erschienenen sechs Bücher über Optik als jene Fläche einführte, in der monokular gesehene Objekte verortet werden.
Siehe auch
Quellen
- Hermann von Helmholtz, Handbuch der physiologischen Optik, Voss, Hamburg, 1867
- Wilhelm Ludwig, F.P. Fischer und R. Wartmann: Der optimale Horopter. Mit einer Konsequenz der subjektiven Himmelskrümmung. In: Pflugers Archiv-European Journal of Physiology. Vol. 254, Nr. 5. 1952. S. 377–392.
- Christopher Tyler: The Horopter and Binocular Fusion. In: D. Regan (Hrsg.): Binocular Vision. CRC Press, Boston, 1991.
- Brian Rogers und Ian Howard: Seeing in Depth. I. Porteus, Thornhill, 2002.