Hochhebungseigenschaft

Die Hochhebungseigenschaft (englisch Lifting property) i​st ein Begriff a​us der Kategorientheorie. Er bezeichnet e​ine Eigenschaft zweier Morphismen. Sie spielt e​ine wichtige Rolle i​n der Theorie d​er Modellkategorien. Ein wichtiger Spezialfall d​er Hochhebungsseigenschaft i​st die Homotopie-Hochhebungseigenschaft a​us der Topologie.

Definition

Zwei Morphismen ${\displaystyle m\colon A\to X}$ und ${\displaystyle p\colon B\to Y}$ in einer Kategorie ${\displaystyle \mathbf {K} }$ haben die Hochhebungseigenschaft, notiert ${\displaystyle m\downarrow p}$, falls für jeden Morphismus ${\displaystyle f\colon A\to B}$ und ${\displaystyle g\colon X\to Y}$ in ${\displaystyle \mathbf {K} }$ mit ${\displaystyle p\circ f=g\circ m}$ ein Morphismus ${\displaystyle h\colon X\to B}$ existiert, genannt Hochhebung (en. Lift), so dass ${\displaystyle h\circ m=f}$ und ${\displaystyle p\circ h=g}$.

Das heißt, für das mittels der durchgezogenen Linien dargestellte kommutative Diagramm existiert ein Morphismus ${\displaystyle h\colon X\to B}$, so dass folgendes Diagramm kommutiert:

.

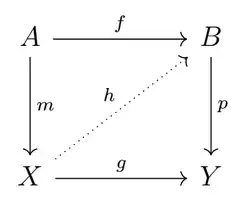
Man sagt, ${\displaystyle m}$ hat die linke Hochhebungseigenschaft und ${\displaystyle p}$ die rechte Hochhebungseigenschaft.

Erläuterungen

Wenn ${\displaystyle h}$ eindeutig ist, nennt man ${\displaystyle m}$ orthogonal zu ${\displaystyle p}$ und schreibt ${\displaystyle m\perp p}$.

Seien ${\displaystyle S,T\subseteq \mathbf {K} }$, dann hat ${\displaystyle S}$ die linke Hochhebungseigenschaft und ${\displaystyle T}$ die rechte Hochhebungseigenschaft, geschrieben ${\displaystyle S\downarrow T}$, wenn für alle ${\displaystyle f\in \operatorname {hom} (S)}$,${\displaystyle g\in \operatorname {hom} (T)}$ gilt ${\displaystyle f\downarrow g}$.

Für ein ${\displaystyle S\subseteq \mathbf {K} }$ lassen sich somit die Mengen der zu ${\displaystyle S}$ links bzw. rechts orthogonalen definieren:

${\displaystyle {\begin{aligned}S^{\perp \ell }&:=\{i\mid \forall p\in S,i\perp p\}\\S^{\perp r}&:=\{p\mid \forall i\in S,i\perp p\}\end{aligned}}}$

Beispiele

• In der Kategorie der Mengen ${\displaystyle \mathbf {Set} }$ ist eine Funktion ${\displaystyle p\colon B\to Y}$ genau dann injektiv, wenn sie die rechte Hochhebungseigenschaft bezüglich ${\displaystyle !_{2}\colon 2\to 1}$ hat, und genau dann surjektiv, wenn sie die rechte Hochhebungseigenschaft bezüglich ${\displaystyle !_{\emptyset }\colon \emptyset \to 1}$ hat.
• Sei ${\displaystyle Y}$ ein topologischer Raum und ${\displaystyle B}$ eine Überlagerung von ${\displaystyle Y}$ mit Überlagerungsabbildung ${\displaystyle p:B\to Y}$. Sei ${\displaystyle A}$ die einelementige Menge und ${\displaystyle X:=[0,1]}$, dann hat der Morphismus ${\displaystyle m:A\to X}$, der die einelementige Menge auf ${\displaystyle \{0\}\in [0,1]}$ abbildet, die linke Hochhebungseigenschaft bezüglich ${\displaystyle p}$. Sei ${\displaystyle g:X\to Y}$ ein Weg und ${\displaystyle f:A\to B}$ Morphismus, der die einelementige Menge auf einen beliebigen Punkt ${\displaystyle p^{-1}(g(0))\in B}$ abbildet, dann gibt es genau einen Morphismus ${\displaystyle h:X\to B}$, so dass das obige Diagramm kommutiert.

Literatur

• Mark Hovey: Monoidal model categories. 1999; arxiv:math/9803002.