Hjelmslev-Ebene

Eine Hjelmslev-Ebene ist eine Inzidenzstruktur, in der zwei Punkte mehrere Verbindungsgeraden und zwei Geraden mehrere Schnittpunkte haben können. Der Name geht auf Johannes Hjelmslev zurück, der die Geometrie des Zeichnens mit Bleistift und Papier axiomatisiert hat.[1] Ein Punkt, der auf Papier gezeichnet wurde, hat immer eine von Null verschiedene Fläche, und je näher zwei Punkte sich sind, desto mehr verschiedene Verbindungsgeraden lassen sich zeichnen. Zwei mit einem Bleistift gezeichnete Geraden, die sich unter einem kleinen Winkel schneiden, schneiden sich tatsächlich offenbar nicht nur in einem Punkt, sondern auf einer ganzen Strecke.

In einer Hjelmslev-Ebene ist auf der Punktmenge ${\mathcal {P}}$ eine Relation benachbart definiert: Man sagt, der Punkt P ist benachbart zum Punkt Q, wenn P und Q mindestens zwei Verbindungsgeraden haben. Entsprechend heißen zwei Geraden g und h benachbart, wenn es zu jedem Punkt P auf g einen Punkt Q auf h gibt, der mit P benachbart ist.

Definition

Eine Inzidenzstruktur ${\mathcal {H}}$ = $\langle {\mathcal {P}},{\mathcal {G}},\mathbf {I} \rangle$ heißt fast-affine Hjelmslev-Ebene, wenn folgende Axiome gelten[2]:

Axiom 1: Zu je zwei Punkten gibt es mindestens eine Verbindungsgerade.

Axiom 2: Wenn die Geraden g und h wenigstens einen Schnittpunkt haben, dann haben sie mehr als einen Schnittpunkt genau dann, wenn sie benachbart sind.

Axiom 3: Es gibt einen Epimorphismus von ${\mathcal {H}}$ auf eine gewöhnliche affine Ebene, so dass

die Bilder zweier Punkte P und Q genau dann gleich sind, wenn P und Q benachbart sind,
die Bilder zweier Geraden g und h genau dann gleich sind, wenn g und h benachbart sind und
die Bilder von g und h parallel sind, wenn g und h keinen Schnittpunkt haben.

Axiom 4: Liegt der Punkt P auf der Geraden g, so ist die Anzahl der Geraden, die durch P gehen und die mit g benachbart sind, von der Wahl von P und g unabhängig.

Parallelrelation

Ist in der fast-affinen Hjelmslev-Ebene ${\mathcal {H}}$ eine Parallelrelation definiert, so dass das Parallelenaxiom gilt, dann nennt man ${\mathcal {H}}$ eine affine Hjelmslev-Ebene. Weil es zu jeder Geraden g und jedem Punkt P, der nicht auf g liegt, mehrere Geraden durch P gibt, die g nicht schneiden, lassen sich in einer fast-affinen Hjelmslev-Ebene mehrere Parallelrelationen definieren. Daher gilt der Satz von Desargues im Allgemeinen nicht. Eine affine Hjelmslev-Ebene lässt sich zu einer projektiven Hjelmslev-Ebene erweitern.[3]

Minimalmodell

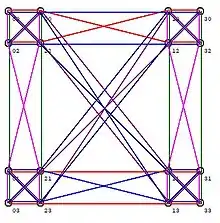
Koordinatisierung

Affine Hjelmslev-Ebenen lassen sich durch einen Ternärkörper koordinatisieren.[4] Ein Minimalmodell einer Hjelmslevebene lässt sich durch den Restklassenring $\mathbb {Z}$ /4 $\mathbb {Z}$ beschreiben.

Einzelnachweise

Hjelmslev, Johannes: Die natürliche Geometrie. In Abh. Math. Sem. Univ. Hamburg. 1923, S. 1–36.
Lüneburg, Heinz: Affine Hjelmslevebenen mit transitiver Translationsgruppe. In: Math. Z. 79. 1962, S. 260–288.
Drake, David Allen: Existence of Parallelisms and Projective Extensions for Strongly n-Uniform Near Affine Hjelmslev Planes. In: Geometriae Dedicata 3. 1974, S. 191–214.
Lorimer, J.W.: Desarguesian Affine Hjelmslev Planes. In: Journal für reine und angewandte Mathematik 278/279. 1975, S. 336–352.

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[1] Hjelmslev, Johannes: Die natürliche Geometrie. In Abh. Math. Sem. Univ. Hamburg. 1923, S. 1–36.

[2] Lüneburg, Heinz: Affine Hjelmslevebenen mit transitiver Translationsgruppe. In: Math. Z. 79. 1962, S. 260–288.

[3] Drake, David Allen: Existence of Parallelisms and Projective Extensions for Strongly n-Uniform Near Affine Hjelmslev Planes. In: Geometriae Dedicata 3. 1974, S. 191–214.

[4] Lorimer, J.W.: Desarguesian Affine Hjelmslev Planes. In: Journal für reine und angewandte Mathematik 278/279. 1975, S. 336–352.