Hinduistischer Lunisolarkalender
Der hinduistische Lunisolarkalender existiert in einer großen Vielfalt und regionalen Varianten. In diesem Artikel werden daher nur die Grundprinzipien dargestellt, die allen Lunisolarkalendern zugrunde liegen.
Geschichte
Die ältesten Hinweise auf Zeitrechnung auf dem indischen Subkontinent gibt es bereits in den Veden, deren älteste Teile bis etwa 1200 v. Chr. zurückreichen. Aus späterer Zeit stammt das Jyotisha Vedanga mit Abhandlungen über Astronomie und Astrologie. Griechische und babylonische Kenntnisse beeinflussten in den ersten Jahrhunderten n. Chr. die Siddhantas (astronomische Lehrbücher). Die drei wichtigsten sind der wohl älteste Surya-Siddhanta, der Arya-Siddhanta des Astronomen Aryabhata I. (476 – um 550 n. Chr.) und der Brahma-Siddhanta des Brahmagupta (598 – 668)[1].
Bis etwa 1100 n. Chr. wurde für die Kalenderberechnung die mittlere Bewegung von Sonne und Mond zugrunde gelegt, später wurde dann auf die scheinbare Bewegung von Sonne und Mond Bezug genommen[2].
Das Jahr
Das Lunisolarjahr ist ein an das siderische Sonnenjahr gebundenes Mondjahr mit zwölf oder dreizehn Monaten. Daraus ergibt sich für ein Gemeinjahr (samvatsara mana) mit zwölf Monaten eine Länge von 354 oder 355 Tagen bzw. für ein Schaltjahr (adhika samvatsara) mit dreizehn Monaten eine Länge von 383, 384 oder 385 Tagen.[3]
Es werden zwei Jahresformen unterschieden. Wenn – wie vor allem im Norden Indiens – die Monate von einem Vollmond bis zum nächsten Vollmond dauern, ist das Jahr ein purnimanta Jahr, wenn – wie vor allem im Süden des Landes – die Monate von einem Neumond bis zum nächsten Neumond dauern, ist das Jahr ein amanta Jahr[4].
Die Jahreszählung
Die Jahre werden nach der Kali Yuga-Ära als abgelaufene Jahre gezählt, nach der Vikrama Samvat-Ära[5] als laufende Jahre.
Der Jahresanfang
Das Jahr beginnt fast überall in Indien mit dem letzten Neumond, bevor die Sonne in das Zeichen mesha (Widder) tritt. Ein solches Jahr wird als chaitrada bezeichnet. In Gujarat beginnt das Jahr mit dem Neumond, bevor die Sonne in das Zeichen tula (Waage) tritt. Ein solches Jahr wird als karttikadi bezeichnet. Da das Jahr stets mit Neumond beginnt, fängt ein purnimanta Jahr daher mitten in einem Monat an.
Die Genauigkeit
Da das Mondjahr an das siderische Jahr gebunden ist, ist es im Durchschnitt so lang, wie das siderische Jahr, dessen Länge der Surya-Siddhanta mit 365,2587558 Tagen angibt. Die anderen Siddhantas geben einen etwas abweichenden Wert an[6]. Da die Länge des siderischen Jahres aber tatsächlich 365,2563042 Tage beträgt, das Surya-Siddhanta Jahr also um 0,0024516 Tage länger ist, verschiebt es sich gegenüber den Fixsternen in rund 400 Jahren um 1°. Während der Bezugspunkt um das Jahr 285 n. Chr.[7] der Stern chaitra (Spica, αVir) war, ist es heute der Stern τVir. Wegen der Präzession der Erdachse verschiebt sich der Frühlingspunkt gegen den Fixsternhimmel, und heute steht die Sonne dem Stern τVir etwa Mitte April gegenüber. Der Jahresanfang des Lunisolarjahres fällt gegenwärtig also in die Zeit zwischen Mitte März und Mitte April. Die folgende Tabelle gibt den Jahresanfang für die nächsten Jahre an. Wegen der vielen Varianten der Kalenderrechnung kann das tatsächliche Datum um ein oder zwei Tage abweichen[8].
| Kali Yuga | Vikrama Samvat | gregorianisch |
|---|---|---|
| 5116 | 2071 | 31. März 2014 |
| 5117 | 2072 | 20. März 2015 |
| 5118 | 2073 | 7. April 2016 |
| 5119 | 2074 | 28. März 2017 |
| 5120 | 2075 | 17. März 2018 |
| 5121 | 2076 | 5. April 2019 |
| 5122 | 2077 | 24. März 2020 |
| 5123 | 2078 | 12. April 2021 |
| 5124 | 2079 | 2. April 2022 |
| 5125 | 2080 | 22. März 2023 |
Der Monat
Der bürgerliche Monat ist vom Mondmonat zu unterscheiden.
Der Mondmonat
Ein Mondmonat beginnt bei Neumond bzw. Vollmond. Wenn der Monat mit Neumond beginnt und endet, ist es ein amana masa, wenn er mit Vollmond beginnt und endet, ist es ein purnimanta masa.
Ein Mondmonat besteht aus 30 Mondtagen (s. unten), die in zwei Hälften zu je 15 Mondtagen geteilt werden: Die helle Hälfte mit zunehmendem Mond, die bei Neumond beginnt und bei Vollmond endet, heißt sukla paksha, die dunkle Hälfte mit abnehmendem Mond, die bei Vollmond beginnt und bei Neumond endet, heißt krishna paksha.
Die 15 Tage der hellen Hälfte werden von 1 bis 15 gezählt und durch ein vorangestelltes „S“ (für sukla – hell) gekennzeichnet; die 15 Tage der dunklen Hälfte werden von 1 bis 14 und der letzte Tag mit 30 gezählt und durch ein vorangestelltes „K“ (für krishna – dunkel) gekennzeichnet. In einem amanta-Monat folgt auf die erste, helle Hälfte die dunkle, zweite Hälfte, woraus sich die Zählung K 30 für den letzten Tag des Monats erklärt.
In einem purnimanta-Monat folgt auf die erste, dunkle Hälfte die helle, zweite Hälfte. Auch hier wird der letzte Tag der dunklen Hälfte K 30 gezählt, obwohl er in die Mitte des Monats fällt[9].
Manchmal werden die einzelnen Mondtage auch mit Namen bezeichnet, die von den indischen Zahlwörtern[10] abgeleitet sind[11]:
| Nr. | Name |
|---|---|
| 1 | pratipadā |
| 2 | dvitīyā |
| 3 | tŗitīyā |
| 4 | chathurtī |
| 5 | panchamī |
| 6 | shasthī |
| 7 | saptamī |
| 8 | ashtamī |
| 9 | navamī |
| 10 | daśamī |
| 11 | ekādasī |
| 12 | dvādasī |
| 13 | trayodasī |
| 14 | chartudasī |
| 15 | pūrņimā |
| 30 | amāvāsyā |
Der bürgerliche Monat
Der bürgerliche Monat beginnt mit Neumond bzw. Vollmond bevor die Sonne in ein neues Sternkreiszeichen tritt (samkranti).
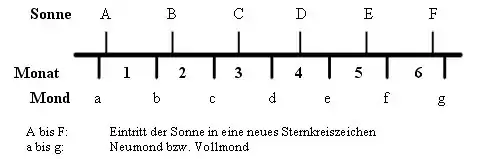 |
Die Sonne braucht im Schnitt 30,43822963 Tage, um durch ein Sternkreiszeichen zu wandern. Wegen ihrer ungleichmäßigen Bewegung schwankt die Zeit aber zwischen 29,34806481 und 31,61057407 Tagen[12]. Der Mond braucht im Schnitt 29,53058796 Tage von Neumond zu Neumond bzw. Vollmond zu Vollmond. Wegen seiner ungleichmäßigen Bewegung schwankt die Zeit aber zwischen 29,246 und 29,817 Tagen[13].
Wegen der unterschiedlichen Dauer kommt es vor, dass ein Mondmonat zu Ende geht, ohne dass die Sonne in ein neues Sternkreiszeichen eingetreten ist. In diesem Fall wird ein zusätzlicher bürgerlicher Monat eingeschaltet und das Jahr umfasst 13 Monate.
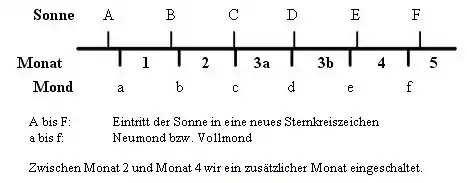 |
Ein eingeschalteter Monat wird als adhika bezeichnet und geht dem eigentlichen (nija) Monat voran.
Außerdem kommt es – wenn auch selten – vor, dass die Sonne während eines Mondmonats ein Sternkreiszeichen vollständig durchwandert und in ein zweites Sternkreiszeichen tritt. In diesem Fall wird ein bürgerlicher Monat ausgeschaltet.
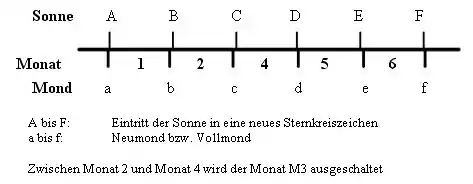 |
Ein ausgeschalteter Monat wird als kshaya bezeichnet Allerdings umfasst ein gebundenes Mondjahr immer 12 oder 13 bürgerliche Monate, so dass zwangsläufig früher oder später mindestens ein bürgerlicher Monat eingeschaltet wird[14]. Der bürgerliche Monat hat eine Länge von 29 oder 30 bürgerlichen Tagen (s. unten).
Die Monatsnamen
Die Monatsnamen sind sehr alt und haben eine lange Tradition Die einzelnen Monate des Jahres haben in einem chaitrada-Jahr folgende Namen[15]:
| Monat | |
|---|---|
| indisch | deutsch |
| चैत्र | Caitra |
| वैशाख | Vaiśākha |
| ज्येष्ठ | Jyeṣṭha |
| आषाढ | Āsādha |
| श्रावण | Śrāvaņa |
| भाद्रपद | Bhādrapada |
| अश्विन् | Āśvina |
| कार्तिक | Kārtika |
| अग्रहायण | Agrahāyaṇa |
| पौष | Pauṣa |
| माघ | Māgha |
| फाल्गुन | Phālguna |
In einem karttikadi-Jahr beginnt das Jahr mit dem Monat Kârttika.
Der Tag
Der Mondtag
Ein Mondmonat ist der vollständige Umlauf des Mondes um die Erde in Bezug auf die Sonne. Bei diesem Umlauf gewinnt der Mond im Laufe eines Mondmonats 360° Abstand zur Sonne. Ein Mondtag (tithi) ist nun die Zeit, in der der Mond jeweils 12° mehr Abstand zur Sonne gewinnt. Ein Mondtag dauert im Schnitt 23,62447222 Stunden.[16]
Der bürgerliche Tag
Der bürgerliche Tag wird nach dem Mondtag gezählt, in den der Sonnenaufgang fällt[17].
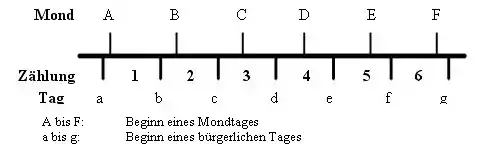 |
Wegen der ungleichmäßigen Bewegung des Mondes ist die Dauer eines Mondtages jedoch sehr unterschiedlich; sie schwankt zwischen 21,57333333 und 26,10666667 Stunden[16]. Wegen der unterschiedlichen Längen von Mondtag und bürgerlichem Tag, kommt es vor, dass ein Mondtag zu Ende geht, ohne dass ein neuer bürgerlicher Tag begonnen hat. In diesem Fall wird bei der Tageszählung ein Tag übersprungen; z. B. folgt auf Mittwoch S 3 Donnerstag S 5.
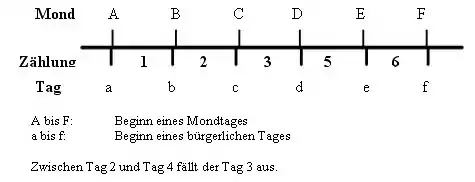 |
Außerdem kommt es vor, dass während eines Mondtages zwei bürgerliche Tage beginnen. In diesem Fall wird bei der Tageszählung ein Tag zweimal gezählt; z. B. folgt auf Dienstag K 3 Mittwoch K 3.
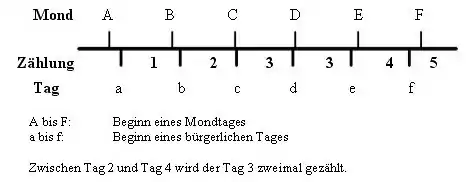 |
Unterteilung des Tages
Der bürgerliche Tag wird in 60 gathas Unterteilt, diese in 60 palas und diese wiederum in 60 vipalas. In der folgenden Tabelle sind gathas und Stunden und ihre Unterteilungen einander gegenübergestellt[18].
| indisch | westlich |
|---|---|
| 1 gathikâ = 60 pala | 24 Minuten |
| 1 pala = 60 vipalas | 24 Sekunden |
| 1 vipala | 0,4 Sekunden |
| westlich | indisch |
| 1 Stunde | 2 1/2 gathikâ |
| 1 Minute | 2 1/2 pala |
| 1 Sekunde | 2 1/2 vipalas |
Nakshatra
Die Bahn, die der Mond in einem siderischen Monat durchläuft und für die der Mond 27,32167361 Tage[12] benötigt, wurde schon in früher Zeit[19] in 27 oder 28 Mondhäuser (nakshatra) unterteilt und nach der Sternkonstellation des jeweiligen Abschnitts benannt. Heute ist eine Einteilung in 27 gleich große Abschnitte von je 13° 20’ üblich. Die Namen der Mondhäuser und ihr Anfangspunkt sind in der folgenden Tabelle zusammengestellt[20].
| Nr. | Name | Anfang | ||
|---|---|---|---|---|
| indisch | Transkription | Grad | Minuten | |
| 1 | अश्विनी | aśvinī | 0° | |
| 2 | भरणी | bharaņī | 13° | 20 |
| 3 | कृत्तिका | kŗttikā | 26° | 40 |
| 4 | रोहिणी | rohiņī | 40° | |
| 5 | म्रृगशीर्षा | mṛgaśīrṣā | 53° | 20 |
| 6 | आद्रा | ārdrā | 66° | 40 |
| 7 | पुनर्वसु | purnavasu | 80° | |
| 8 | पुष्य | pushya | 93° | 20 |
| 9 | आश्ळेषा | âśhleshâ | 106° | 40 |
| 10 | मघा | maghâ | 120° | |
| 11 | पूर्व फाल्गुनी | pûrvaphâlgunî | 133° | 20 |
| 12 | उत्तर फाल्गुनी | uttaraphâlgunî | 146° | 40 |
| 13 | हस्त | hastâ | 160° | |
| 14 | चित्रा | chitrâ | 173° | 20 |
| 15 | स्वाति | svâti | 186° | 40 |
| 16 | विशाखा | viśâkhâ | 200° | |
| 17 | अनुराधा | anurâdhâ | 213° | 20 |
| 18 | ज्येष्ठा | jyeshthâ | 226° | 40 |
| 19 | मूल/मूळ | mûlam | 240° | |
| 20 | पूर्वाषाढा | pûrvaashâdhâ | 253° | 20 |
| 21 | उत्तराषाढा | uttaraashâdhâ | 266° | 40 |
| 22 | श्रवण | śravaņa | 280° | |
| 23 | श्रविष्ठा | śravishţhâ | 293° | 20 |
| 24 | शतभिषक् | śatabhishaj | 306° | 40 |
| 25 | पूर्वभाद्रपदा | pûrvabhâdrapada | 320° | |
| 26 | उत्तरभाद्रपदा | uttarabhâdrapada | 333° | 20 |
| 27 | रेवती | revatî | 346° | 40 |
Yoga
Ein yoga ist die Zeit, in der sich Sonne und Mond zusammen um insgesamt 13°20’ bewegen, also um die Länge eine Mondhauses. Entsprechend gibt es 27 yogas. Ein yoga dauert im Schnitt 22,59575 und schwankt zwischen 20,88 und 24,60667 Stunden[21]. Die Namen der yogas sind in der folgenden Tabelle zusammengestellt[22]
| Nr. | Name |
|---|---|
| 1 | vishkambha |
| 2 | prîti |
| 3 | ayushmat |
| 4 | saubhâgya |
| 5 | śobhana |
| 6 | atigaņda |
| 7 | sukarman |
| 8 | dhŗiti |
| 9 | śūla |
| 10 | gaņda |
| 11 | vŗiddhi |
| 12 | dhruva |
| 13 | vyâghâta |
| 14 | harshaņa |
| 15 | vajra |
| 16 | siddhi |
| 17 | vyatîpâta |
| 18 | varîyas |
| 19 | parigha |
| 20 | śiva |
| 21 | siddha |
| 22 | sādhya |
| 23 | śubha |
| 24 | śukla |
| 25 | brahman |
| 26 | indra |
| 27 | vaidhŗti |
Karana
Ein karana ist die Zeit, in der der Mond ein halbes Mondhaus durchwandert, also ein halbes tithi. Neben vier festen Bezeichnungen (1/1, 29/2, 30/1 und 30/2) gibt es sieben Namen, die sich mehrfach wiederholen. Die folgende Tabelle gibt die Bezeichnungen der 30 karanas und ihre Zuordnung zu den tithis an[23]:
| tithi | 1. Hälfte. | 2. Hälfte. | tithi | 1. Hälfte. | 2. Hälfte | ||||
|---|---|---|---|---|---|---|---|---|---|
| Nr. | indisch | Transskiption | indisch | Transskiption | Nr. | indisch | Transskiption | indisch | Transskiption |
| 1 | किंस्तुघ्न | kiṃstughna | बव | bava | 16 | बालव | bālava | कौलव | kaulava |
| 2 | बालव | bālava | कौलव | kaulava | 17 | तैतिल | taitila | गरज | gara |
| 3 | तैतिल | taitila | गरज | gara | 18 | वणिज | vaņij | भद्रा | viṣhţi |
| 4 | वणिज | vaņij | भद्रा | viṣhţi | 19 | बव | bava | बालव | bālava |
| 5 | बव | bava | बालव | bālava | 20 | कौलव | kaulava | तैतिल | taitila |
| 6 | कौलव | kaulava | तैतिल | taitila | 21 | गरज | gara | वणिज | vaņij |
| 7 | गरज | gara | वणिज | vaņij | 22 | भद्रा | viṣhţi | बव | bava |
| 8 | भद्रा | viṣhţi | बव | bava | 23 | बालव | bālava | कौलव | kaulava |
| 9 | बालव | bālava | कौलव | kaulava | 24 | तैतिल | taitila | गरज | gara |
| 10 | तैतिल | taitila | गरज | gara | 25 | वणिज | vaņij | भद्रा | viṣhţi |
| 11 | वणिज | vaņij | भद्रा | viṣhţi | 26 | बव | bava | बालव | bālava |
| 12 | बव | bava | बालव | bālava | 27 | कौलव | kaulava | तैतिल | taitila |
| 13 | कौलव | kaulava | तैतिल | taitila | 28 | गरज | gara | वणिज | vaņij |
| 14 | गरज | gara | वणिज | vaņij | 29 | भद्रा | viṣhṭi | शकुनि | śakuni |
| 15 | भद्रा | viṣhṭi | बव | bava | 30 | चतुष्पाद | chatuṣhpada | नाग | nâga |
Die Woche
Die Woche
Die Wocheneinteilung ist babylonisch-griechischen Ursprungs. Die Namen sind von den entsprechenden Gottheiten abgeleitet. Die Namen sind in der folgenden Tabelle zusammengestellt:
| indisch | gregorianisch | |
|---|---|---|
| रविवार | Ravivār | Sonntag |
| सोमवार | Somavār | Montag |
| मंगलवार | Mangalavār | Dienstag |
| बुधवार | Budhavār | Mittwoch |
| गुरूवार | Guruvār | Donnerstag |
| शुक्रवार | Shukravār | Freitag |
| शनिवार | Shanivār | Samstag |
Der Kalender (panchanga)
Ein Panchanga (wörtlich: fünf Teile), der traditionelle Hindu-Kalender, gibt für jeden Tag außer dem Wochentag für die Zeit des Sonnenaufgangs auch tithi, nakshatra, yoga und karana[18] an.
Literatur
- Friedrich Karl Ginzel Handbuch der mathematischen und Technischen Chronologie. Bd. 1: Zeitrechnung der Babylonier, Ägypter, Mohammedaner, Perser, Inder, Südostasiaten, Chinesen, Japaner und Zentralamerikaner, Leipzig 1906 [Reprint der Originalausgabe, Universität Innsbruck, o. J.] – (online in Internet Archive)
- Robert Sewell / Sankara Balkrishna Dikshit, The Indian Calendar, London 1896 (als PDF-Datei)
- Edward M. Reingold / Nachum Dershowitz, Calendrical Calculations – The Millennium Edition, Cambridge 2001 (englisch)
- Reingold / Nachum Dershowitz, Indian Calendrical Calculations (als PDF-Datei) (englisch)
- Leow Choon Lian, Indian Calendars, National University of Singapore, 2000/2001 (als PDF-Datei) (englisch)
Weblinks
Einzelnachweise
- Friedrich Karl Ginzel: Handbuch der mathematischen und Technischen Chronologie. Bd. 1, Leipzig 1906, S. 334 f
- Edward M. Reingold / Nachum Dershowitz: Calendrical Calculations - The Millennium Edition, Cambridge 2001, S. 127
- Friedrich Karl Ginzel: Handbuch der mathematischen und Technischen Chronologie. Bd. 1, Leipzig 1906, S. 351
- Friedrich Karl Ginzel: Handbuch der mathematischen und Technischen Chronologie. Bd. 1, Leipzig 1906, S. 347
- Leow Choon Lian: Indian Calendars, National University of Singapore, 2000/2001, S. 36
- Friedrich Karl Ginzel: Handbuch der mathematischen und Technischen Chronologie. Bd. 1, Leipzig 1906, S. 341
- Edward M. Reingold / Nachum Dershowitz, Indian Calendrical Calculations (Memento des Originals vom 21. März 2015 im Internet Archive) Info: Der Archivlink wurde automatisch eingesetzt und noch nicht geprüft. Bitte prüfe Original- und Archivlink gemäß Anleitung und entferne dann diesen Hinweis., S. 14
- Details of years, abgerufen am 9. November 2014.
- Leow Choon Lian: Indian Calendars, National University of Singapore, 2000/2001, S. 40f.
- Menninger: Zahlwort und Ziffer, Vandenhoeck & Ruprecht, Göttingen 1958, Band 1, S. 103
- Friedrich Karl Ginzel: Handbuch der mathematischen und Technischen Chronologie. Bd. 1, Leipzig 1906, S. 348f.
- Friedrich Karl Ginzel: Handbuch der mathematischen und Technischen Chronologie. Bd. 1, Leipzig 1906, S. 342.
- Leow Choon Lian: Indian Calendars, National University of Singapore, 2000/2001, S. 38.
- Leow Choon Lian: Indian Calendars, National University of Singapore, 2000/2001, S. 42
- Friedrich Karl Ginzel: Handbuch der mathematischen und Technischen Chronologie. Bd. 1, Leipzig 1906, S. 320
- Friedrich Karl Ginzel: Handbuch der mathematischen und Technischen Chronologie. Bd. 1, Leipzig 1906, S. 349.
- Leow Choon Lian: Indian Calendars, National University of Singapore, 2000/2001, S. 41
- Robert Sewell / Sankara Balkrishna Dikshit: The Indian Calendar, London 1896, S. 2.
- Robert Sewell / Sankara Balkrishna Dikshit, The Indian Calendar, London 1896, S. 21
- Friedrich Karl Ginzel: Handbuch der mathematischen und Technischen Chronologie. Bd. 1, Leipzig 1906, S. 328
- Robert Sewell / Sankara Balkrishna Dikshit, The Indian Calendar, London 1896, S. 3
- Friedrich Karl Ginzel: Handbuch der mathematischen und technischen Chronologie, Leipzig 1906, Bd. I, Seiten 361f.
- Friedrich Karl Ginzel: Handbuch der mathematischen und Technischen Chronologie. Bd. 1, Leipzig 1906, S. 360