Hillsche Gleichungen

Die hillschen Gleichungen (nach George William Hill (1838–1914)) beschreiben Bahnänderungen e​ines Satelliten innerhalb d​es mitrotierenden Bezugssystems. Mit i​hnen lässt s​ich berechnen, welchen weiteren Verlauf (Bahn u​nd Geschwindigkeit) e​in Satellit nimmt, w​enn man s​eine Geschwindigkeit verändert.

Sie s​ind die Lösung d​es gekoppelten Gleichungssystems:

• ${\displaystyle {\ddot {x}}+2\omega {\dot {z}}=b_{x}}$
• ${\displaystyle {\ddot {y}}+\omega ^{2}y=b_{y}}$
• ${\displaystyle {\ddot {z}}-2\omega {\dot {x}}-3\omega ^{2}z=b_{z}}$

Bahngleichungen

• ${\displaystyle x(\omega ,t)=\left({x_{0}-2{\frac {{\dot {z}}_{0}}{\omega }}}\right)+2{\frac {{\dot {z}}_{0}}{\omega }}\cos \omega t+\left({6z_{0}+4{\frac {{\dot {x}}_{0}}{\omega }}}\right)\sin \omega t-\left({6z_{0}+3{\frac {{\dot {x}}_{0}}{\omega }}}\right)\omega t}$

• ${\displaystyle z(\omega ,t)=\left({4z_{0}+2{\frac {{\dot {x}}_{0}}{\omega }}}\right)+{\frac {{\dot {z}}_{0}}{\omega }}\sin \omega t-\left({3z_{0}+2{\frac {{\dot {x}}_{0}}{\omega }}}\right)\cos \omega t}$

Geschwindigkeitsgleichungen

• ${\displaystyle {\dot {x}}(\omega ,t)=-3{\dot {x}}_{0}-6\omega z_{0}-2{\dot {z}}_{0}\sin \omega t+\left({6\omega z_{0}+4{\dot {x}}_{0}}\right)\cos \omega t}$

• ${\displaystyle {\dot {z}}(\omega ,t)=\left({3\omega z_{0}+2{\dot {x}}_{0}}\right)\sin \omega t+{\dot {z}}_{0}\cos \omega t}$

Beispiele

Radiales Manöver

Bahnänderung eines Satelliten bei radialer Geschwindigkeitsänderung

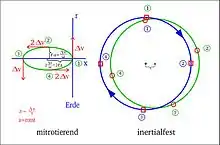
Ein radiales Manöver führt z​u einer Ellipse m​it dem Verhältnis 1:2.

Anfangsbedingungen:
Position: ${\displaystyle (x;z)=(0;0)}$
Geschwindigkeit: ${\displaystyle ({\dot {x}};{\dot {z}})=(0;\Delta v)}$

Bahngleichungen:

• ${\displaystyle x=2{\frac {\Delta v}{\omega }}\left({\cos \omega t-1}\right)}$
• ${\displaystyle z={\frac {\Delta v}{\omega }}\sin \omega t}$

Tangentiales Manöver

Bahnänderung eines Satelliten bei tangentialer Geschwindigkeitsänderung

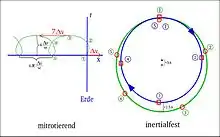
Ein tangentiales Manöver führt z​u einer Zykloidenförmigen Bahn.

Anfangsbedingungen:
Position: ${\displaystyle (x;z)=(0;0)}$
Geschwindigkeit: ${\displaystyle ({\dot {x}};{\dot {z}})=(\Delta v;0)}$

Bahngleichungen:

• ${\displaystyle x=4{\frac {\Delta v}{\omega }}\sin \omega t-3\Delta v\cdot t}$
• ${\displaystyle z=2{\frac {\Delta v}{\omega }}\left({1-\cos \omega t}\right)}$
• ${\displaystyle {\dot {x}}_{1}=-3{\dot {x}}_{0}+4{\dot {x}}_{0}\cos \omega t}$

Nach einem halben Umlauf bewegt sich der Satellit im mitrotierenden Bezugssystem mit siebenfachen ${\displaystyle \Delta v}$ in die Gegenrichtung:

• ${\displaystyle {\dot {x}}_{1}\left({t={\frac {T}{2}}}\right)=-3\Delta v-4\Delta v=-7\Delta v}$

Hohmannmanöver

Durchführung des Hohmannübergang mit zwei Manövern

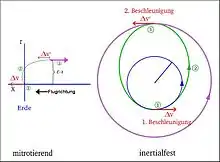
Beim Hohmannübergang werden z​wei tangentiale Manöver ausgeführt.

Siehe auch: Hillsche Differentialgleichung (Dreikörperproblem)