Graphpartitionierung
Graphpartitionierung bezeichnet die Anwendung geeigneter Algorithmen zur Berechnung von Graphpartitionen (vgl. Schnitt (Graphentheorie)) mit gewünschten Eigenschaften. Ein Graph heißt r-partit, wenn eine Partition (Teilung) seiner Knoten in r Teile existiert, so dass die Endecken jeder Kante des Graphen in verschiedenen Partitionsklassen liegen.[1]
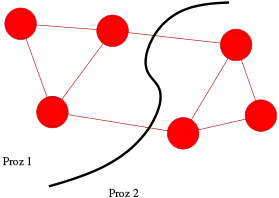
Graphpartitionierung in der parallelen Programmierung
Formulierung des Problems
Graphpartitionierung findet vor allem in der Parallelverarbeitung Verwendung: Um in einem rechenintensiven Computerprogramm die Vorteile eines parallelen Systems optimal ausnutzen zu können, muss dieses zwei Kriterien erfüllen:
- Die Rechenlast muss gleichmäßig auf die Recheneinheiten verteilt werden.
- Die zur Abarbeitung des Programms nötige Kommunikation zwischen den Recheneinheiten soll möglichst klein gehalten werden, da diese immense Ausführungszeit beansprucht.
Das Optimierungsproblem als Graphpartitionierungsproblem
Dieses Optimierungsproblem lässt sich als Graph-Partitionierungsproblem formulieren:
- Die einzelnen Berechnungsaufgaben im Programm werden als Knoten eines Graphen modelliert.
- Für jede Berechnung, welche vom Resultat einer anderen Berechnung abhängig ist, werden die entsprechenden Knoten mit einer Kante verbunden.
- Nach dem Partitionieren spiegeln die berechneten Teilmengen des Graphen die Prozessoren wider, auf welche die Aufgaben verteilt werden sollen.
Damit lautet das Optimierungsproblem neu: Finde eine Partition des gegebenen Graphen so, dass:
- Die Knoten gleichmäßig auf die Teilmengen verteilt sind.
- Möglichst wenig Kanten Knoten aus zwei verschiedenen Teilmengen verbinden.
Kanten, deren adjazente Knoten in unterschiedlichen Teilmengen liegen, werden durch die Partition geschnitten und deshalb als Schnittkanten bezeichnet.
Gewichtete Graphen
Man kann das Optimierungsproblem auch für gewichtete Graphen formulieren. Damit lassen sich unterschiedlich intensive Rechenaufgaben durch verschiedene Knotengewichte darstellen. Ebenso kann durch gewichtete Kanten der Datenaustausch von unterschiedlichen Datenmengen modelliert werden. Das Optimierungsproblem heißt also allgemeiner:
- Das Knotengewicht gleichmäßig auf die Teilmengen aufteilen und
- die Summe der Gewichte der geschnittenen Kanten minimieren.
Die Summe der Gewichte der geschnittenen Kanten wird auch als Schnittgröße (englisch cutsize, edge-cut) bezeichnet. Die obige, spezielle Formulierung des Optimierungsproblems ist mit diesem äquivalent, wenn alle Kanten und Knoten das Gewicht 1 erhalten.
Beispiel
In der obigen Abbildung wurde ein (ungewichteter) Graph mit sechs Knoten und acht Kanten in zwei Teile geschnitten, zu je drei Knoten. Eine Teilmenge wird Prozessor 1 zugewiesen, die andere Prozessor zwei. Dabei werden zwei Kanten geschnitten, was einen gewissen Kommunikationsaufwand bedeutet. Es existiert keine andere gleichmäßige Verteilung der Knoten, die nicht mehr als zwei Schnittkanten bewirken würde. Somit ist diese Partition optimal.
Algorithmen
Die optimale Partition für einen Graphen zu berechnen, ist ein NP-vollständiges Problem. Deshalb existiert eine Reihe von vorgeschlagenen Heuristiken, um in kurzer Zeit wenigstens annähernd optimale Partitionen zu finden.
Diese lassen sich in etwa gliedern nach den Ansätzen, die sie verfolgen:
Rekursive Bisektion
Dieses Verfahren kann in allen der im Folgenden erwähnten Algorithmen angewendet werden. Es verfolgt das verbreitete Divide-and-conquer-Prinzip und besteht darin, dass der Graph nur in 2 Teilmengen geschnitten wird. Die entstehenden Teilgraphen werden dann rekursiv wieder zweigeteilt, bis die gewünschte Anzahl k von Teilmengen erreicht ist. Diese Zahl muss somit eine Zweierpotenz sein, d. h. für ein (= Rekursionstiefe). Das ist in der Praxis in der Tat oft der Fall, z. B. in einem Parallelrechner, der Prozessoren enthält.
Durch Anwendung von rekursiver Bisektion nimmt man eine suboptimale Lösung in Kauf, um einen großen zeitlichen Gewinn zu erzielen.
Geometrische Algorithmen
Geometrische Algorithmen machen Gebrauch von Koordinateninformationen der Knoten. Ein Graph besitzt als solches keine Koordinaten. Bei manchen Anwendungsbereichen wird der Graph aber aus einem zwei- oder dreidimensionalen Netz gebildet. Das ist z. B. der Fall, wenn in einer physikalischen Simulation ein reelles Objekt mittels eines Netzes modelliert wird, an welchem dann Berechnungen in jedem Knoten durchgeführt werden sollen. Meist sind diese jeweils nur von den Resultaten der benachbarten Knoten abhängig, so dass das Netz direkt als Graph für die Partitionierung übernommen werden kann. Die Koordinateninformationen solcher Netze widerspiegeln dann ziemlich gut die Topologie des Graphen.
Beispiele für geometrische Algorithmen:
- Koordinatenbisektion: Wähle die Koordinate (z. B. x), in welcher die Knoten am weitesten voneinander entfernt sind, und für diese einen Grenzwert c so, dass für die Hälfte der Knoten (x > c) gilt.
- Inertialbisektion: Berechne die Inertialachse und wähle diese anstelle einer Koordinatenachse.
Spektrale Bisektion
Die Idee der spektralen Bisektion ist, das (diskrete) Optimierungsproblem mathematisch in einem stetigen Gleichungssystem zu formulieren und die Lösung analytisch herzuleiten. Danach versucht man, die Lösung des stetigen Gleichungssystems diskret anzunähern.
Kombinatorische Algorithmen
Für Graphpartitionierung ohne Koordinateninformation gibt es eine Reihe kombinatorischer Algorithmen, welche hier nur namentlich erwähnt werden:
- Graph growing
- Greedy-Algorithmen
- Kernighan-Lin/Fidduccia-Mattheyses
Multilevel-Partitionierung

Die Idee hierbei ist, einen großen Graphen mittels sogenannter Matchings zusammenzuschrumpfen zu einem kleineren, welcher die globale Struktur des ursprünglichen repräsentiert. Diese Schrumpfung (englisch coarsening) wird mehrmals wiederholt, bis nur noch wenige (z. B. weniger als 100) Knoten vorhanden sind. Danach wird der kleinste Graph partitioniert. Die Partitionierung wird auf den nächstgrößeren Graphen zurückgerechnet und dort z. B. mittels Kernighan-Lin optimiert (englisch refinement), danach wieder auf den nächstgrößeren Graphen zurückgerechnet, bis man beim ursprünglichen Graphen gelandet ist. Mit diesem Schema wird sowohl die lokale als auch die globale Topologie des Graphen berücksichtigt, was zu sehr guten Ergebnissen führt.
Streaming-Algorithmen
Bei diesem Ansatz werden die Kanten oder Knoten des Graphen in einer beliebigen Reihenfolge eingelesen und sequentiell anhand einer Heuristik-Funktion auf die Partitionen verteilt. Durch diesen Ansatz ist es nicht nötig, den gesamten Graphen im Speicher zu halten, wie im Fall des Multilevel-Verfahrens. Außerdem haben Streaming-Algorithmen aufgrund ihrer einfachen Heuristik eine geringe Latenz. Werden Knoten gestreamt, spricht man von Edge-Cut, im Fall von Kanten spricht man von Vertex-Cut. Beispiele für Streaming-Algorithmen sind:
- HDRF
- Greedy
Ein besonderer Ansatz wird durch den ADWISE[2] -Algorithmus verfolgt. Er ist ein Streaming-Algorithmus, verwendet aber gleichzeitig einen Kanten-Buffer. Dadurch kann der Algorithmus im Rahmen der Buffergröße seine Kantenzuweisungen optimieren. Über die Buffergröße lässt sich außerdem die Laufzeit des Algorithmus beeinflussen. Je größer der Buffer, desto besser ist die berechnete Partitionierung, allerdings führt dies dann auch zu mehr Latenz.
Literatur
- Aydin Buluc, Ilya Safro, Henning Meyerhenke, Peter Sanders, Christian Schulz: Recent Advances in Graph Partitioning. 2013, arxiv:1311.3144.
- Christian Schulz: High Quality Graph Partitioning. epubli GmbH, Berlin 2013, ISBN 978-3-8442-6462-3 (Online [PDF] Dissertation, Karlsruhe Institute of Technology).
- U. Elsner: Graph partitioning – a survey. 1997 (englisch).
Einzelnachweise
- Diestel, Reinhard.: Graphentheorie. 3., neu bearb. und erw. Auflage. Springer, Berlin 2006, ISBN 3-540-21391-0, S. 18.
- Christian Mayer, Ruben Mayer, Muhammad Adnan Tariq, Heiko Geppert, Larissa Laich, Lukas Rieger, Kurt Rothermel: ADWISE: Adaptive Window-based Streaming Edge Partitioning for High-Speed Graph Processing. (PDF) Universität Stuttgart, abgerufen am 27. Juli 2018 (englisch).
- Christian Schulz: High Quality Graph Partitioning. Dissertation. Karlsruhe Institute of Technology, 2013.
- Peter Sanders, Christian Schulz: Engineering Multilevel Graph Partitioning Algorithms. In: Proceedings of the 19th European Symposium on Algorithms (ESA’11). volume 6942 of LNCS, pages 469--480. Springer, 2011.
- Peter Sanders, Christian Schulz: Distributed Evolutionary Graph Partitioning. In: Proceedings of the 12th Workshop on Algorithm Engineering and Experimentation (ALENEX’12). S. 16–19, 2012.
- Peter Sanders, Christian Schulz: High Quality Graph Partitioning. In: Proceedings of the 10th DIMACS Implementation Challenge Workshop: Graph Partitioning and Graph Clustering. S. 1–17, AMS, 2013.
- http://algo2.iti.kit.edu/documents/kahip/index.html
- G. Karypis, V. Kumar: A fast and high quality multilevel scheme for partitioning irregular graphs. SIAM Journal on Scientific Computing 20 (1): S. 359. (1999)
- http://glaros.dtc.umn.edu/gkhome/metis/metis/overview
- http://www.labri.fr/perso/pelegrin/scotch/