Glitch (Elektronik)
In der Elektronik bezeichnet man mit Glitch [glɪtʃ] eine kurzzeitige Falschaussage in logischen Schaltungen und temporäre Verfälschung einer booleschen Funktion. Diese tritt auf, weil die Signallaufzeiten in den einzelnen Gattern niemals vollkommen gleich sind. Diese Verfälschung wird daher auch als Race Condition bezeichnet. Die Anfälligkeit für Glitches steigt mit der Komplexität, der Geschwindigkeitserhöhung und der Verkleinerung der Schaltungen, kann aber auch bereits bei sehr einfachen Schaltungen vorhanden sein. Sie stellen ein wesentliches Problem bei der Entwicklung moderner elektronischer Schaltungen und schneller Mikroprozessoren dar, das war aber auch schon bei der älteren elektromechanischen Relaistechnik so.
Ein Glitch wird manchmal auch als Hazard (engl.: „Gefahr, Risiko, Zufall“) oder Spike (engl.: „Spitze, Dorn“) bezeichnet.
Wortherkunft
Laut einschlägigen Nachschlagwerken, etwa Random House's American Slang, kommt der Begriff vom deutschen Wort glitschen über das jiddische gletshn („schlittern oder rutschen“) in das Englische. Es ist jedenfalls ein ziemlich neuer Begriff, der erstmals am 20. Juni 1965 von Bennett Cerf für das amerikanische Publikum in der Sendung What's My Line wie folgt definiert wurde: „Wenn in Cape Kennedy etwas schief läuft, dann sagen sie, es sei zu einem unbedeutenden Glitch gekommen.“ Der Astronaut John Glenn erklärte den Begriff in seinem Buch Into Orbit folgendermaßen:
Ein anderes Wort, das wir verwendeten, um einige unserer Probleme zu beschreiben, war "Glitch". Genaugenommen ist ein Glitch der Spannungswechsel in einem Stromkreis, zu dem es kommt, wenn dem Stromkreis plötzlich ein neuer Abnehmer hinzugefügt wird. Ihnen ist wahrscheinlich schon das kurze Schwächerwerden der Lichter in Ihrem Haushalt aufgefallen, wenn sie etwas einschalten oder den Trockner oder den Fernsehapparat aufdrehen. Normalerweise werden diese Spannungsschwankungen von Sicherungen abgefangen. Ein Glitch jedoch ist eine derart kleine Stromschwankung, dass keine Sicherung davor schützen kann.[1]
John Daily definierte den Begriff in der Ausgabe vom 4. Juli 1965 derselben Sendung weiters als Wort, das von der Air Force in Cape Kennedy im Zuge der Raketenstarts dann verwendet wird, wenn etwas schiefläuft und man nicht wirklich feststellen kann warum; dies sei es, was dann ein Glitch genannt wird. Das Time Magazine vom 23. Juli 1965 führte in einem Artikel aus: Glitch sei das Wort von Raumfahrern für irritierende Turbulenzen. Der Begriff ist dann während des Wettlaufs ins All der 1960er Jahre in die Alltagssprache übergegangen, wo es kleinere Fehler in der Hardware bezeichnete, die nur schwer ausfindig gemacht werden konnten.[2][3]
Beispiel
Erklärung der Schaltsymbole → siehe: Logikgatter#Typen von Logikgattern und Symbolik
| Grafik 1 – die Schaltung
Es sei eine Schaltung gegeben, die drei Eingänge besitzt: x0, x1 und x2. Sie soll den Wert „1“ liefern, wenn mindestens eine der beiden Bedingungen erfüllt ist:
Trifft nicht wenigstens eine der beiden Bedingungen zu, soll sie „0“ ausgeben. | |
| Situation 1 – Die Schaltung liefert wie gewünscht eine 1
Die Schaltung befinde sich jetzt in Situation 1. Laut unseren Vorgaben ist die erste Bedingung erfüllt, nämlich x1 und x0 sind „1“. Die Verzweigungen, die die Information „1“ tragen, sind rot dargestellt. Der Inverter wandelt die eingehende „1“ in eine „0“ um. Daher lässt das nachfolgende Und-Glied kein Signal mehr durch, gibt also eine „0“ aus. Die gesamte Schaltung (ODER-Glied) liefert aber dennoch eine „1“, da das andere UND-Glied die „1“ liefert. | |
| Situation 2 – Inverter verursacht einen Glitch
In Situation 2 soll x1 = 0 und x2 = 1 sein. Die Schaltung soll weiterhin eine „1“ ausgeben. Der Inverter benötigt allerdings eine gewisse Zeit, um die Umwandlung des x1-Signals von "0" in eine „1“ wahrzunehmen. Für kurze Zeit ist sowohl x1 = 0, als auch (x1)’ = 0. Dieser Umstand wird so verarbeitet, als ob keine der Bedingungen erfüllt ist und gibt folglich eine „0“ aus. Diese Situation bezeichnet man als Glitch. | |
| Situation 3 – Die Schaltung gibt wieder den korrekten Wert aus
Nach einiger Zeit – in der Größenordnung von Nanosekunden – befindet sich die Schaltung in Situation 3: der Inverter hat die neue Information verarbeitet. Die jetzt ausgegebene „1“ läuft in das UND-Gatter, welches (wieder nach kurzer Verzögerung) dann auch eine „1“ liefert. Die gesamte Schaltung liefert nun die gewünschte „1“. |
Unterscheidungen
Funktions- und Struktur-Glitches
Funktionshazards entstehen durch den gleichzeitigen Belegungswechsel von mehr als einer Variable. Diese Hazards können durch geeigneten Belegungswechsel (Gray-Codierung), durch Taktung oder durch eine Verzögerung (RC-Glied am Ausgang) vermieden werden.
Strukturhazards entstehen bei Schaltungen mit mehr als einer Stufe durch den Wechsel von einem Block im KV-Diagramm (= Gatter in der Schaltung) in einen angrenzenden Block (keine überlappende Blöcke im KV-Diagramm). Diese Hazards können vermieden werden durch die Realisierung redundanter Primkonjunktionen (überlappende Blöcke im KV-Diagramm) oder durch Taktung.
Nach dieser Nomenklatur handelt es sich bei dem oben gegebenen Beispiel um einen Strukturhazard.
Statische und dynamische Glitches
Es gibt zwei Arten von Glitches: statische und dynamische. Statisch ist ein Glitch dann, wenn kein Wechsel im Ausgabewert erfolgen soll, der Glitch aber kurzzeitig den anderen Wert liefert. Ein dynamischer Glitch springt dagegen nach einem Wechsel auf den neuen Wert noch einmal kurz auf den alten zurück.
Je nachdem, ob der Glitch beim Wechsel auf eine 1 oder auf eine 0 stattfindet, unterscheidet man weiterhin 0-Glitches oder 1-Glitches.
Bedeutung von Glitches
In der Praxis existieren Laufzeitunterschiede auch in Gattern desselben Typs oder in den unterschiedlich langen Leitungen. Möchte man den exakten Wert der Funktion wissen, muss man eine entsprechende Zeit warten bis alle Glitches beseitigt sind. Diese Tatsache beschränkt wesentlich die Taktfrequenz moderner Prozessoren.
Beseitigung
Ein wichtiges Hilfsmittel zum Entwurf von Schaltfunktionen sind die Karnaugh-Diagramme. Im Prinzip ist es also möglich, auch größere Schaltungen ohne Glitches zu realisieren. Man benötigt dazu aber weitere Komponenten in der Schaltung und schon bei etwas komplexeren Aufbauten wird deren Zahl enorm groß, was die Schaltung verteuert. Es gilt einen guten Kompromiss zu finden zwischen den Kosten des Schaltkreises und der Dauer der Glitches.
Vermeiden der Auswirkung
D-Flip-Flops
Die Auswirkungen von Glitches können in synchronen Schaltungsdesigns durch nachgeschaltete D-Flipflops verhindert werden. Die Idee dabei ist, dass die Ausgänge der kombinatorischen Schaltungsteile, bestehend aus diversen Gattern unterschiedlicher Laufzeit, erst dann gültige Zustände annehmen müssen, wenn die Taktflanke die Ausgangswerte in die D-Flipflops übernimmt. In der Zeit zwischen zwei Taktflanken können im kombinatorischen Teil durch Laufzeiteffekte beliebig viele Glitches auftreten, da diese Zwischenzustände nicht durch das nachgeschaltete D-Flipflop beachtet werden. Der Nachteil ist, dass als kleinste Zeiteinheit die Taktperiode des D-Flipflops auftritt und kein zeitkontinuierliches Ausgangssignal wie bei einer rein kombinatorischen Schaltung mehr vorliegt.
Das Verfahren, die Ausgänge von kombinatorischen Schaltungsteilen immer mit D-Flipflops zu versehen, ist eine der wesentlichen Grundlagen für stabile, digitale Schaltungsdesigns in komplexen, freiprogrammierbaren FPGAs.
Angleichung der Verzögerungszeiten
Im obigen Beispiel könnte dieses Vorgehen darin bestehen, in den oberen Zweig der vom Eingang x1 ausgehenden Leitung ein weiteres (funktionsloses) Gatter einzufügen, damit die Signaländerung die beiden UND-Gatter gleichzeitig erreicht. Dieses Verfahren ist allerdings mit einigen Unsicherheiten behaftet und liefert nicht sicher das gewünschte Ergebnis.
Systematische Vorgehensweise
Die bessere Methode ist die systematische Vorgehensweise. Dazu optimiert man das der betreffenden Schaltung zugrundeliegende KV-Diagramm. Das zum obigen Beispiel gehörende Diagramm zeigt zwei Blöcke, die durch die beiden UND-Gatter realisiert sind (Disjunktive Normalform). Der Hazard entsteht beim Übergang zwischen diesen beiden Blöcken. Aufgelöst wird der Hazard, wenn man diesen Übergang mit einem weiteren, von der Logik her überflüssigen, Block überbrückt, der sich mit beiden Blöcken überlappt: x0 und x2 sind gleichzeitig „1“. In der resultierenden Schaltung muss dann entsprechend ein weiteres UND-Gatter eingefügt werden. Die Schaltung kann dann aber statisch nicht mehr vollständig getestet werden, da ein fehlerhaftes UND-Gatter nicht auffällt. Der Hazard kann bei den heutigen Gatterlaufzeiten messtechnisch nicht aufgenommen werden.
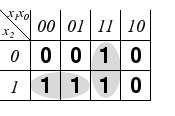 KV-Diagramm der hazardbehafteten Schaltung |
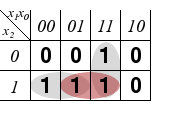 Auflösung des Hazards im KV-Diagramm |
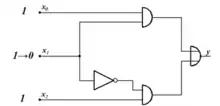 Schaltnetz mit Hazard |
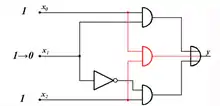 Schaltnetz mit aufgelöstem Hazard durch zusätzliches Gatter |
Zu beachten ist allerdings, dass sich nicht nur unterschiedliche Laufzeiten von einzelnen Gattern in Form von Glitches auswirken können, sondern auch die unterschiedlich langen Laufzeiten der Signale in den Verbindungsleitungen. Dazu müssen die einzelnen Verbindungsleitungen mit Hilfe der Leitungstheorie modelliert werden. Diese Laufzeiten werden bei der systematischen Auflösung mittels KV-Diagrammen nicht beachtet. Daher ist dieses Verfahren nur verwendbar bei vergleichsweise niedrigen Schaltfrequenzen (=quasistationärer Fall) bzw. diskreten Schaltungsteilen, die mit entsprechend abgestimmten Verbindungsleitungen betrieben werden. Bei hohen Signalraten, wobei 100 MHz als grober Richtwert verwendet werden kann, und wenn auf die konkrete Signalführung (z. B. bei einer Verschaltung innerhalb von FPGAs) vom Entwickler nur geringer Einfluss genommen werden kann, liefern auch aufgelöste kombinatorische Schaltungen keine glitch-freien Designs.
Siehe auch
Weblinks
Einzelnachweise
- Ben Zimmer, "The Hidden History of Glitch," visualthesarus.com The Hidden History of "Glitch". Abgerufen am 30. Juni 2017.
- Dictionary.com. Abgerufen am 15. Oktober 2012.
- Online Etymology Dictionary. Abgerufen am 15. Oktober 2012.