Gift-Wrapping-Algorithmus
Der Gift-Wrapping-Algorithmus, auch Jarvis-March genannt, ist ein Algorithmus zur Berechnung der konvexen Hülle einer Punktemenge im zweidimensionalen Raum. Er wurde 1973 von R. A. Jarvis veröffentlicht. Der Algorithmus gehört zu den „ausgabesensitiven“ (englisch output-sensitive) Algorithmen.
Beschreibung
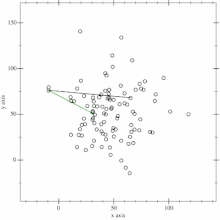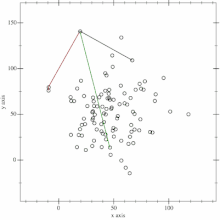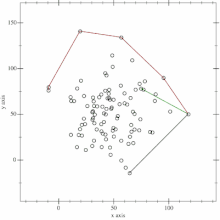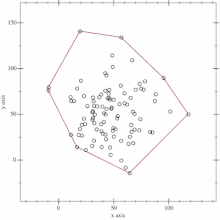
Gegeben sei eine Menge von Punkten in einer Ebene. Als Startpunkt wird der Punkt mit der kleinsten Ordinate gewählt. Sind dies mehrere, so wird aus diesen der Punkt mit der kleinsten Abszisse gewählt. Der Startpunkt ist somit Teil der konvexen Hülle. Nun wird ein beliebiger Punkt aus der Menge gewählt, mit welchem der Startpunkt eine Gerade bildet. Als nächstes werden die restlichen Punkte aus der Menge überprüft, ob ein Punkt links dieser Geraden liegt. Rechts und links ergeben sich in diesem Zusammenhang aus dem Winkel zwischen dem Richtungsvektor der Trennungsgeraden und dem Vektor definiert durch den Anfangspunkt der Geraden und den zu überprüfenden Punkt. Ist dieser Winkel kleiner als 180°, dann wird der Punkt als rechts von der Geraden betrachtet, bei Winkeln größer 180° als links von ihr. Wird ein Punkt links der Geraden gefunden, bildet mit diesem eine neue Gerade. Anschließend wird der Rest der Menge überprüft. Für jeden Punkt, der links von dieser Geraden liegt, wird dieser Vorgang wiederholt. Wurden alle Punkte überprüft, ist der zuletzt gefundene Punkt der nächste Punkt auf der konvexen Hülle. Nun wird als neuer Startpunkt gewählt und der gesamte Vorgang wiederholt, bis wieder der Startpunkt ist.
Für jeden Punkt auf der konvexen Hülle muss die komplette Menge durchlaufen werden. Dieser Teil wird in einer Schleife ausgeführt, wobei jeder Schleifendurchlauf eine Laufzeit von besitzt. Sei die Anzahl der Punkte auf der konvexen Hülle, ergibt sich eine Laufzeit von . Im Worst Case, wenn alle Punkte auf der konvexen Hülle liegen, ergibt sich somit eine Laufzeit von . Da der Algorithmus von der Anzahl der Punkte auf der konvexen Hülle abhängt, gehört er zu den sogenannten ausgabesensitiven Algorithmen.
Pseudocode

jarvis(S)
startpunkt = Punkt mit kleinster Ordinate
i = 0
wiederhole
P[i] = startpunkt
endpunkt = S[0]
wenn startpunkt == endpunkt
endpunkt = S[1]
für j von 1 bis |S|
ist (endpunkt == startpunkt) oder (S[j] links von der Geraden zwischen startpunkt und endpunkt)
endpunkt = S[j]
startpunkt = endpunkt
i++
bis endpunkt == P[0]
Programmierung
Das folgende Beispiel in der Programmiersprache C# zeigt die Implementierung des Gift-Wrapping-Algorithmus. Die Punkte und die konvexe Hülle werden auf dem Hauptfenster gezeichnet. Das Programm verwendet mehrere Klassen. Die Methoden für den eigentlichen Algorithmus werden in der Klasse GiftWrapping deklariert.[1][2]
| Code-Schnipsel |
using System;
using System.Collections.Generic;
using System.Drawing;
using System.Windows.Forms;
public class GiftWrapping
{
// Diese Methode bestimmt die Orientierung des drei Punkte. Wenn die Punkte im Uhrzeigersinn sind, wird ein Wert größer als 0 zurückgegeben. Wenn die Punkte im Gegenuhrzeigersinn sind, wird ein Wert kleiner als 0 zurückgegeben. Wenn die Punkte kollinear sind, wird der Wert 0 zurückgegeben.
public int GetOrientation(Point point1, Point point2, Point point3)
{
return (point2.Y - point1.Y) * (point3.X - point2.X) - (point2.X - point1.X) * (point3.Y - point2.Y);
}
// Diese Methode gibt eine Liste der Punkte der konvexen Hülle zurück
public List<Point> GetConvexHull(List<Point> points)
{
List<Point> convexHull = new List<Point>();
int numberOfpoints = points.Count;
if (numberOfpoints < 3) // Wenn weniger als 3 Punkte vorhanden sind, wird eine leere Liste zurückgegeben
{
return convexHull;
}
float minimumX = points[0].X;
int indexOfMinimum = 0;
// Diese for-Schleife durchläuft die verbleibenden Punkte und ermittelt den Punkt ganz links und bei Gleichheit den untersten Punkt
for (int i = 1; i < numberOfpoints; i++)
{
float x = points[i].X;
if (x < minimumX || minimumX == x && points[i].Y < points[indexOfMinimum].Y)
{
minimumX = points[i].X;
indexOfMinimum = i;
}
}
int currentIndex = indexOfMinimum;
int nextIndex;
// Diese do-while-Schleife beginnt beim Punkt ganz links und läuft im Gegenuhrzeigersinn, bis sie wieder den Anfangspunkt erreicht. Die Anzahl der Durchläufe der Schleife ist die Anzahl der Punkte der konvexen Hülle.
do
{
convexHull.Add(points[currentIndex]); // Fügt den aktuellen Punkt der Liste der Punkte der konvexen Hülle hinzu
nextIndex = (currentIndex + 1) % numberOfpoints; // Erhöht den Index nextIndex um 1 und setzt ihn zurück auf 0, wenn der maximale Wert überschritten ist
// Diese for-Schleife durchläuft alle Punkte und sucht einen Punkt mit Index nextIndex, sodass die Punkte mit den Indexen currentIndex, nextIndex, x für alle Indexe x im Gegenuhrzeigersinn sind
for (int i = 0; i < numberOfpoints; i++)
{
if (GetOrientation(points[currentIndex], points[nextIndex], points[i]) < 0) // Wenn der Punkt mit Index i weiter im Gegenuhrzeigersinn liegt als der Punkt mit Index nextIndex, wird nextIndex aktualisiert
{
nextIndex = i;
}
}
// Der Punkt mit Index nextIndex ist der Punkt, der in Bezug auf den Punkt mit Index currentIndex am weitesten im Gegenuhrzeigersinn liegt. Nach der folgenden Zuweisung wird dieser Punkt der konvexen Hülle hinzugefügt.
currentIndex = nextIndex;
}
while (currentIndex != indexOfMinimum); // While we don't come to first
return convexHull;
}
}
// Klasse für das Hauptfenster
public partial class MainForm : Form
{
private Graphics graphics;
private List<Point> points = new List<Point>(); // Liste der Punkte
private List<Point> convexHull = new List<Point>(); // Liste der Punkte der konvexen Hülle
private double x1, y1, x2, y2;
public MainForm()
{
x1 = 100; y1 = 100; x2 = 700; y2 = 700; // Setzt die Koordinaten der Eckpunkte der quadratischen Zeichenfläche
Random random = new Random(); // Initialisiert den Zufallsgenerator
int numberOfPoints = 100;
for (int i = 0; i < numberOfPoints; i++) // Diese for-Schleife erzeugt 100 zufällige Punkte innerhalb der quadratischen Zeichenfläche
{
Point point = new Point();
point.X = (int)(random.NextDouble() * (x2 - x1) + x1);
point.Y = (int)(random.NextDouble() * (y2 - y1) + y1);
points.Add(point); // Fügt den Punkt der Liste hinzu
}
GiftWrapping giftWrapping = new GiftWrapping(); // Erzeugt ein Objekt der Klasse GiftWrapping
convexHull = giftWrapping.GetConvexHull(points); // Aufruf der Methode, die die konvexe Hülle zurückgibt
InitializeComponent();
Text = "Konvexe Hülle";
Width = 800;
Height = 800;
graphics = CreateGraphics(); // Erzeugt ein Grafikobjekt für das Zeichnen auf dem Hauptfenster.
Paint += OnPaint; // Verknüpft die Ereignisbehandlungsmethode mit dem Paint Ereignis des Hauptfensters.
}
// Diese Methode wird aufgerufen, wenn das Hauptfenster gezeichnet wird.
private void OnPaint(object sender, PaintEventArgs e)
{
for (int i = 0; i < points.Count; i++)
{
graphics.FillRectangle(new SolidBrush(Color.FromArgb(0, 0, 0)), points[i].X - 1, points[i].Y - 1, 2, 2); // Zeichnet die Punkte
}
int numberOfPoints = convexHull.Count;
for (int i = 0; i < numberOfPoints; i++)
{
graphics.DrawLine(new Pen(Color.FromArgb(0, 0, 255)), convexHull[i], convexHull[(i + 1) % numberOfPoints]); // Zeichnet die Kanten der konvexen Hülle
}
}
}
|
Literatur
- Jarvis, R. A.: On the identification of the convex hull of a finite set of points in the plane. In: Information Processing Letters. 2, 1973, S. 18–21. doi:10.1016/0020-0190(73)90020-3.
Weblinks
Einzelnachweise
- OpenGenus IQ: Gift Wrap Algorithm (Jarvis March Algorithm) to find Convex Hull
- GeeksforGeeks: Convex Hull