Frequenzbesen
Der Frequenzbesen ist ein Element von Testbildern und dient der Beurteilung der horizontalen und der vertikalen Auflösung eines wiedergegebenen Fernsehbildes. Die Bezeichnung bezieht sich auf die Ähnlichkeit mit einem Strauch- oder Rutenbesen.
Ein Frequenzbesen besteht aus nebeneinander liegenden schmalen Sektoren oder Dreiecken, die abwechselnd weiß und schwarz sind und mit der Spitze auf einen gemeinsamen Punkt zulaufen. Zur Spitze hin verschwimmt das Muster, weil die nahe beisammenstehenden hellen und dunklen Bereiche nicht mehr getrennt dargestellt werden können. Je geringer die Auflösung des Bildes, umso größer der Bereich, in dem das Muster verschwimmt.
Die Darstellung des Frequenzbesens mit senkrecht verlaufenden Dreiecken wird vor allem durch die Bandbreite des Fernsehsignals und der Elektronik bestimmt; dafür ist neben dem Frequenzbesen klein die Bandbreite in MHz angegeben. Sobald die Sektoren so schmal sind, dass sie zu einer einheitlichen Graufläche verschwimmen, ist die Bandbreite erreicht.
Der Frequenzbesen mit waagrecht liegenden Dreiecken gibt vor allem über die Auflösung der Bildröhre (Fokussierung) Auskunft. Die Frequenzangaben beziehen sich hier nicht auf die im realen Fernsehsignal vorhandenen spektralen Anteile. Es handelt sich um jene Frequenzen, die zu übertragen wären, wenn der Frequenzbesen um 90° gedreht wäre. Hier ist die bei manchen Testbildern als Zeilenanzahl angegebene Auflösung aussagekräftiger („Z“ im Beispielsbild). Die Besen nahe den Bildecken dienen der Beurteilung der Randunschärfe der Bildröhre.
Bei verkleinerten Bildern von Frequenzbesen kann auch der Moiré-Effekt sichtbar sein: Nahe der Spitze erscheint es, als ob die Sektoren gebogen wären. Es handelt sich um eine Interferenz zwischen der Ortsfrequenz der Vorlage und der Ortsfrequenz der diskreten Abtastung.
In neueren, elektronisch erzeugten Testbildern wurden die Frequenzbesen zur Bestimmung der Bandbreite durch Frequenzpakete (oder Wobbelbänder) ersetzt; die Besen mit waagrecht liegenden Dreiecken sind entfallen, weil sie nur solche Frequenzen betreffen, deren Übertragung nicht in Frage steht.
Der Frequenzbesen als theoretisches Modell
isolierter horizontaler Frequenzbesen
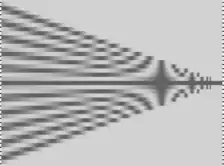Frequenzbesen nach Diskretisierung
derselbe Frequenzbesen nach versuchter Rekonstruktion, rechts der Mitte kommt es zum Aliasing und zu falschen Rekonstruktionen zu niedrigeren Frequenzen
Betrachtet werden hier horizontale Frequenzbesen, also solche, die Aufschluss über die vertikale Auflösung liefern. Vertikale Frequenzbesen sind natürlich völlig analog zu behandeln.
Betrachtet man einen senkrechten Schnitt durch das Signal, so ergibt sich ein Rechtecksignal mit nach rechts hin zunehmender vertikaler Ortsfrequenz (und abnehmender Ausdehnung, da die Anzahl der Besenstriche konstant bleibt). Übersteigt dieser die vertikale Auflösung der Aufnahme, Übertragung oder Anzeige, so ist eine korrekte Wiedergabe nicht mehr gewährleistet. Typischerweise wird also der linke Teil des Besens korrekt wiedergegeben, und an der horizontalen Position des Auftretens erster Irregularitäten, in obigen Beispielen in etwa ab der Bildmitte, kann man so die Auflösung der Darstellung ablesen. Traditionelles Samplingwissen empfiehlt zum verhindern solcher Artefakte deswegen eine vorherige Tiefpassfilterung bis zur größten unterstützten Frequenz.
Im ersten hier gezeigten Bild ist die kritische Auflösung die vertikale Auflösung des gespeicherten Thumbnails bzw., bei Vergrößerung, des gespeicherten Bildes. Wir gehen hier zunächst nicht von einem rechteckförmigen, sondern von einem sinusförmigen Signal aus, da das natürlich mathematisch die Zuordnung zu einer bestimmten vertikalen Frequenz erleichtert.
Die Beschränkung der Auflösung wird hier, wie beim Fernsehsignal, durch Diskretisierung realisiert. Im dargestellten Bild entsprechen 15 vertikale Pixel (Originalgröße) einer Zeile, die horizontale Breite des korrekt wiedergegebenen Bereichs reduziert sich also durch die Diskretisierung erheblich.
Um zu demonstrieren, inwieweit jeweils das ursprüngliche Signal rekonstruiert werden kann, verwenden wir das Nyquist-Shannon-Abtasttheorem. Dieses besagt, dass wenn das Spektrum des vertikalen Schnitts auf das Frequenzband bis zur halben vertikalen Abtastfrequenz beschränkt ist, eine vollständige Rekonstruktion des Signals mittels vertikaler Faltung mit der Sinc-Funktion (Si-Funktion oder auch Spaltfunktion) möglich ist. Versuchen wir diese Rekonstruktion am betrachteten Beispiel, erhalten wir das oben dargestellte Ergebnis. Man erkennt klar die Kante, ab der die Voraussetzung des Abtasttheorems nicht mehr erfüllt ist, da die vertikale Ortsfrequenz des Schnittes zu hoch wird.
Beim Übergang zu Rechtecksignalen ist zu beachten, dass diese auch die dritte, fünfte usw. Oberschwingung enthalten. Die Rekonstruktion erschwert sich dadurch erheblich, da nun das Signal (theoretisch) noch nicht einmal bandbeschränkt ist. Rechts abgebildet ist die Rekonstruktion bei einem Signal, das nur bis zur fünften Oberschwingung an das Rechtecksignal angenähert ist. Man erkennt, wie sich nun nach rechts hin schrittweise die Darstellungsqualität verschlechtert, da immer weniger Oberschwingungen korrekt rekonstruiert werden können.