Fizeau-Interferometer
Ein Fizeau-Interferometer[1] (benannt nach seinem Erfinder Hippolyte Fizeau) ist ein spezielles Interferometer, das unter anderem für die Beurteilung der optischen Qualität von Oberflächen und Optiken genutzt wird. Dazu wird eine definierte Oberfläche mit Hilfe der Interferenz von Licht mit einer anderen Oberfläche verglichen.
Aufbau und Funktionsweise
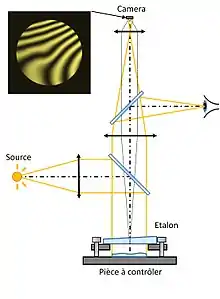
Ein Fizeau-Interferometer für die Beurteilung opaker Oberflächen ist wie folgt aufgebaut. Monochromatisches Licht (z. B. Laserlicht) wird über einer Objektivlinse und einer Lochblende „gefiltert“. Die Lochblende befindet sich im Fokus (Brennpunkt) einer zweiten Linse, der Kollimationslinse. Zwischen der Blende und der zweiten Linse befindet sich ein Strahlteiler.
Der kolliminierte Strahl trifft nun auf eine Glasplatte, deren zur Kollimationslinse zeigende Oberfläche von guter optischer Qualität ist. Die andere Oberfläche ist von außerordentlicher Qualität, eine sogenannte λ/20-Oberfläche oder besser ist notwendig. Sie dient als Referenzfläche, durch die ein Teil des Lichts reflektiert wird. Der transmittierte Anteil geht weiter zur Probenfläche. Der von der Probenfläche reflektierte Anteil enthält Informationen über die durch die Probe verursachte Aberration. Die Wellenfronten beider Anteile interferieren im Interferometer und werden über den Strahlteiler auf einen Bildschirm oder Detektor geleitet. Das aufgenommene Bild zeigt nun ein scharfes Bild der Probenfläche, das mit einem Streifenmuster (dem Interferenzmuster) durchzogen ist. Dabei zeigt ein durchgehender Streifen Bereiche gleicher Luftspaltdicke an. Angrenzende Streifen hingegen zeigen eine Änderung der Dicke an, die der halben Wellenlänge des Lichts entsprechen.[2]
Der Aufbau eines Fizeau-Interferometers ist vergleichbar mit dem eines Fabry-Pérot-Interferometers, das ebenfalls aus zwei teilweise reflektierenden Flächen besteht. In einem Fizeau-Interferometer jedoch sind die beiden Flächen in der Regel weniger reflektierend (Reflexionsgrad rund 4–30 %), so dass sekundäre Reflexionen weniger zum Randkontrast beitragen.
Die Lichtsäume sind leicht zu interpretieren, und die Unterschiede von weniger als λ/20 einer Wellenlänge können visuell gemessen werden. Das klassische Streifenmuster, das durch ein Fizeau-Interferometer erzeugt wird, sind Newtonsche Ringe, deshalb wird es manchmal auch als Newton-Interferometer bezeichnet. Diese werden durch den Vergleich einer konvexen Kugel mit einer ebenen Probenoberfläche erzeugt.[2]
Der Strahlteiler hat im Unterschied zu anderen Interferometern keine interferometrische Funktion. Des Weiteren ist er nicht um 45° gegenüber dem kollimierten Strahl verdreht. Daraus ergeben sich ein paar praktische Vorteile:[3] Der Strahlteiler
- besitzt eine einfache und robuste Bauweise,
- kann bei gleicher Apertur kleiner als bei anderen Interferometern sein – und somit auch das Interferometer,
- ist leichter auszurichten (justierungsunempfindlich).
Anwendung
Fizeau-Interferometer werden üblicherweise zur Messung der Form einer optischen Oberfläche verwendet (z. B. der Parallelität). In der Regel wird dabei eine Linse oder Spiegel mit einem Vergleichsstück gleicher Form oder Oberflächengüte verglichen. Manchmal wird das Vergleichsstück durch ein diffraktives optisches Element realisiert, da diese durch fotolithografische Methoden gefertigt werden können und eine höhere Präzision bei der Herstellung ermöglichen. Fizeau-Interferometer werden auch in faseroptischen Sensoren zur Messung von Druck, Temperatur, Dehnung etc. eingesetzt.
Auch in Interferenzmikroskopen werden häufig Fizeau-Interferometer eingesetzt.[4]
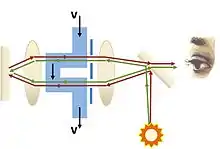
Mit einem abgewandelten Fizeau-Interferometer kann auch der Einfluss der Bewegung eines Mediums (wie Wasser) auf die Lichtgeschwindigkeit gemessen werden. Wie in der nebenstehende Grafik dargestellt wird durch einen gekippten Strahlteiler reflektiert und mit Hilfe einer Linse und einem Spalt in zwei parallele Strahlen aufgespalten. Die Strahlen durchqueren jeweils einen anderen Teil eines Rohres, in dem sich Wasser bewegt. Nach der Durchquerung werden beide Strahlen durch eine weitere Linse so an einem Spiegel reflektiert, dass jeder Strahl den Weg des jeweils anderen Strahls zurück nimmt. Die beiden Strahlen werden am Detektor kombiniert und bilden ein Interferenzmuster, das vom Gangunterschied bei ihrem Weg durch das Wasser abhängt.[5]
Literatur
- Joseph M. Geary: Introduction to optical testing. SPIE Press, 1993, ISBN 978-0-8194-1377-2 (eingeschränkte Vorschau in der Google-Buchsuche).
- P. Hariharan: Optical interferometry. Academic Press, 2003, ISBN 978-0-12-311630-7 (eingeschränkte Vorschau in der Google-Buchsuche).
- P. Hariharan: Basics of interferometry. Academic Press, 2007, ISBN 978-0-12-373589-8 (eingeschränkte Vorschau in der Google-Buchsuche).
- Gerd Litfin: Technische Optik in der Praxis. Springer, 2004, ISBN 978-3-540-21884-5, S. 52 (eingeschränkte Vorschau in der Google-Buchsuche).
Einzelnachweise
- Peter R. Lawson: Principles of Long Baseline Stellar Interferometry. In: Course notes from the 1999 Michelson Summer School, 15.–19. August 1999. National Aeronautics and Space Administration, Jet Propulsion Laboratory, California Institute of Technology, Pasadena, CA, 2000.
- Bass Michael, Decusatis Casimer, Enoch Jay: Handbook of Optics. Volume I: Geometrical and Physical Optics, Polarized Light, Components and Instruments. 3. Auflage. McGraw Hill Professional, ISBN 978-0-07-149889-0.
- Michael Bass: Handbook of optics,Volume II: Design, Fabrication, and Testing; Sources and Detectors; Radiometry and Photometry. 3. Auflage. McGraw Hill Professional, 2009, ISBN 978-0-07-149890-6, S. 13.9 (eingeschränkte Vorschau in der Google-Buchsuche).
- Reinhart Poprawe: Lasertechnik für die Fertigung: Grundlagen, Perspektiven und Beispiele für den innovativen Ingenieur. Springer, 2004, ISBN 978-3-540-21406-9 (eingeschränkte Vorschau in der Google-Buchsuche).
- Robert Williams Wood: Physical Optics. The Macmillan Company, 1905, S. 514 (eingeschränkte Vorschau in der Google-Buchsuche).