Fehlerbaumanalyse

IEC 61025
Bereich	Maschinenbau und Messwesen
Titel	Fehlzustandsbaumanalyse
Kurzbeschreibung:	Wahrscheinlichkeit eines Ausfalls
Letzte Ausgabe	Dezember 2006
Nationale Normen	EN 61025:2007-04,; DIN EN 61025:2007-08,; ÖVE/ÖNORM EN 61025:2007-09-01,; SN EN 61025:2007-04

Die Fehlerbaumanalyse, auch Fehlzustandsbaumanalyse, englisch Fault Tree Analysis (FTA), ist ein Verfahren zur Zuverlässigkeitsanalyse von technischen Anlagen und Systemen. Sie basiert auf der booleschen Algebra und dient dazu, die Wahrscheinlichkeit eines Ausfalls einer Anlage oder Gesamtsystems zu bestimmen. Sie ist eine Art der Systemanalyse und je nach Anwendungsbereich in verschiedenen Spezifikationen wie der NUREG–0492 im Bereich der Nuklearindustrie und bei der NASA[1] und im Bereich der Luftfahrt Teil der ARP4761 von der SAE International. Als internationaler Standard IEC 61025 (EN 61025) ist das Verfahren unter dem Begriff Fehlerzustandsbaumanalyse von der International Electrotechnical Commission beschrieben.[2] In Deutschland ist die Fehlerbaumanalyse Inhalt der nationalen DIN EN 61025.[3]

Im Rahmen der Fehlerbaumanalyse werden die logischen Verknüpfungen von Teilsystemausfällen auf allen kritischen Pfaden ermittelt, welche zu einem Gesamtsystemausfall führen. Das Gesamtsystem wird im Rahmen der Analyse in Minimalschnitte unterteilt; dies sind Ereigniskombinationen, die zu einem Gesamtausfall führen können. Die Anzahl der Minimalschnitte kann je nach Anwendung bis zu einige Millionen Ereigniskombinationen umfassen, die Erstellung komplexer Fehlerbäume und deren Auswertung erfolgt mit speziellen Softwarepaketen. Beispielhafte Anwendungsbereiche der Fehlerbaumanalyse stellen die Luft- und Raumfahrttechnik und die probabilistische Sicherheitsanalyse in der Kernkraftwerkstechnik dar.

Geschichte

Entwickelt wurde die Fehlerbaumanalyse Anfang der 1960er Jahre von H. A. Watson bei den Bell Laboratories zur Sicherheitsbewertung des Abschusskontrollsystems für die von Boeing hergestellte Interkontinentalrakete vom Typ LGM-30 Minuteman. In den Folgejahren wurde bei Boeing die Fehlerbaumanalyse auch beim Entwurf von kommerziellen Flugzeugen eingesetzt.[4] In den 1970er und 1980er Jahren wurde die Fehlerbaumanalyse unter anderem bei der Planung von Atomkraftwerken eingesetzt, in diesem Zeitbereich entstanden auch erste kommerzielle Softwarepakete zur FTA. In der weiteren Folge kamen Einsatzbereiche bei Automobilherstellern und deren Zulieferern hinzu. Letzte Entwicklungen betreffen die dynamische Fehlerbaumanalyse, in deren Rahmen die zeitliche Reihenfolge von Ausfällen und Abhängigkeiten von Basisereignissen modelliert werden können.[5]

Verfahren

Im Rahmen der Fehlerbaumanalyse wird eine sogenannte negative Logik verwendet, d. h. der Fehlerbaum beschreibt eine Ausfallsfunktion, die bei dem Zustand logisch-1 einen Ausfall ausdrückt, bei logisch-0 liegt ein funktionsfähiges System vor. Da sich die Fehlerbaumanalyse der Booleschen Algebra bedient, kann sich das Gesamtsystem oder Teilsysteme wie Komponenten jeweils nur in den beiden Zuständen Funktionsfähig (logisch-0) oder Ausgefallen (logisch-1) befinden.

Ausgegangen wird nach einer Systemanalyse von einem einzigen unerwünschten Ereignis, welches an der Spitze des Fehlerbaums steht, das sogenannte Top-Ereignis, welches beispielsweise den Gesamtausfall des zu betrachtenden Systems beschreibt und im Rahmen einer Gefahrenanalyse ermittelt wird. Je nach Aufgabenstellung kann dieses Top-Ereignis auf bestimmte Randbedingungen eingeschränkt sein, in der Luftfahrttechnik beispielsweise auf katastrophale Zustände, in welchen der unkontrollierbare Absturz des Luftfahrzeuges Folge ist.

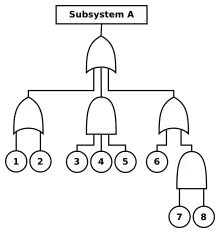
Einfacher Fehlerbaum mit den als Gatter dargestellten logischen Verknüpfungen und acht verschiedenen Basisereignissen, die zu einem Ausfall von Subsystem A führen

Ausgehend von diesem Top-Ereignis wird der Fehlerbaum in einer Top-down Analyse bis zu den einzelnen Ausfallzuständen der Komponenten erstellt. Bei komplexeren Systemen erfolgt die Unterteilung in Subsysteme, welche analog weiter unterteilt werden, bis das komplette System in Form von nicht mehr weiter unterteilbaren Minimalschnitten in Form von Basisereignissen abgebildet ist. Die Ausfallkombinationen im Fehlerbaum werden mit der booleschen Algebra und deren Symbolen, insbesondere dem Und und Oder, logisch verknüpft.

Im einfachsten Fall werden Komponenten eines Systems, welche in ihrer Funktionsfähigkeit voneinander abhängen, durch die logische ODER-Funktion verknüpft. In diesem Fall führt bereits der Ausfall einer Komponente zu einem Ausfall des gesamten Systems. Komponenten, die sich wechselseitig in der Funktion ersetzen können (Redundanz), werden durch die UND-Funktion im Fehlerbaum verknüpft. In komplexen Systemen können auch redundanzübergreifende Fehler auftreten, dies sind Fehlerquellen die an mehreren Stellen des Fehlerbaums auftreten und sich aufgrund der Systemstruktur nicht direkt in einen Minimalschnitt zusammenfassen lassen. Diese sogenannten „Gemeinsam verursachte Fehler“ (GVA) englisch Common Cause Failure, (CCF) erschweren die Analyse.

Systemkomponenten werden im Fehlerbaum üblicherweise in drei Fehlerkategorien unterteilt, die über ein Oder-Gatter verknüpft werden:[6]

Primärausfall: Ausfall der Systemkomponente durch technisches Versagen bei sonst zulässigen Einsatzbedingungen, beispielsweise Materialversagen der Systemkomponente.
Sekundärausfall: Ausfall der Systemkomponente bedingt durch unzulässige Einsatz- und/oder Umgebungsbedingungen, beispielsweise Betrieb bei unzulässiger Umgebungstemperatur.
Kommandierter Ausfall: eine funktionsfähige Systemkomponente, welche zu einem falschen Zeitpunkt oder am falschen Ort aktiviert oder deaktiviert wird, beispielsweise durch Ausfall einer Hilfsenergieversorgung oder einer fehlerhaften Ansteuerung über eine Schnittstelle.

Berechnung

Nach Erstellung des Fehlerbaums wird bei der quantitativen Fehlerbaumanalyse jedem Basisereignis eine bestimmte Eintrittswahrscheinlichkeit für den Ausfall zugewiesen. Daten für konkrete Ausfallsraten können aus eigenen Untersuchungsreihen für die einzelnen Basiskomponenten stammen, oder es wird bei handelsüblichen Bauelementen und Komponenten auf freie Datenbanken wie das MIL-HDBK-217F oder kommerzielle Datenbanken wie 217Plus zurückgegriffen.[7][8] In die Ermittlung der Eintrittswahrscheinlichkeiten können dabei auch Umgebungsbedingungen wie spezielle Temperaturbereiche, geplante Einsatzzeiten, Wartungsintervalle und Ähnliches mehr einfließen.

Die den einzelnen Basiskomponenten zugewiesenen Ausfallraten λ lassen sich im einfachen Fall einer Exponentialverteilung – dies entspricht einer angenommenen zeitlich konstanten Ausfallsrate über die Zeit $t$ – mit der Ausfallwahrscheinlichkeit $P$ ausdrücken als:

P=1-e^{-\lambda t}

was für hinreichend kleine Werte von λt < 0,1 in Näherung

P\approx \lambda t

entspricht. Die Werte im Fehlerbaum werden im Normalfall auf ein bestimmtes, fixes Zeitintervall bezogen. Dieses Intervall für die Normierung kann je nach System unterschiedlich gewählt werden, beispielsweise bei einem Flugzeug auf eine Flugstunde bezogen sein. Die Eintrittswahrscheinlichkeiten sind damit von der Wahl dieses Zeitintervalls abhängig.

Die Ausfallswahrscheinlichkeiten werden in der Fehlerbaumanalyse mit den Symbolen von logischen Gattern zueinander in Bezug gesetzt. Ein UND-Gatter verknüpft zwei statistisch unabhängige Ereignisse an seinen beiden Eingängen $P(A)$ und $P(B)$ und bildet an seinen Ausgang die Wahrscheinlichkeit, dass beide Systeme ausgefallen sind:

P(A\,{\textrm {und}}\,B)=P(A\cap B)=P(A)\cdot P(B)

Ein ODER-Gatter entspricht im Fehlerbaum der Funktion:

P(A\,{\textrm {oder}}\,B)=P(A\cup B)=P(A)+P(B)-P(A)\cdot P(B)

und bildet die Wahrscheinlichkeit, wenn eines der beiden oder beide Basiskomponenten ausgefallen ist. Damit lassen sich iterativ die einzelnen Ausfallswahrscheinlichkeiten im Baum bis zu dem Top-Ereignis berechnen. Spezielle Fälle wie „Gemeinsam verursachte Fehler“ (GVA) bedingen erweiterte Modelle. Im Regelfall werden, vor allem bei komplexen Systemen, auch verschiedene Vereinfachungen bei der Berechnung vorgenommen. So wird unter anderem aufgrund der im Allgemeinen kleinen Eintrittswahrscheinlichkeiten angenommen, dass ein Systemausfall nicht durch gleichzeitigen Ausfall mehrerer Minimalschnitte erfolgt, wodurch bei der Berechnung der Gesamtausfallswahrscheinlichkeit die Terme höherer Ordnung vernachlässigbar sind. Zur Auswertung komplexer Fehlerbäume ist spezielle Software verfügbar, welche die grafische Erstellung, Berechnung und Auswertung erleichtert.

Literatur

Facharbeitskreis Probabilistische Sicherheitsanalyse für Kernkraftwerke, Methoden zur probabilistischen Sicherheitsanalyse für Kernkraftwerke (PDF; 2,72 MB), Dez. 1996, BfS-KT-16-97
Daten zur Quantifizierung von Ereignisablaufdiagrammen und Fehlerbäumen. März 1997, BfS-KT-18/97
Reinhard Böhnert: Bauteil- und Anlagensicherheit. Vogel, Würzburg 1992, ISBN 3-8023-0468-3
Andreas Thums: Formale Fehlerbaumanalyse (PDF; 1,86 MB), Dissertation an der Universität Augsburg, 2004
Siegfried Altmann: Bewertung der Elektrosicherheit – Eine Einführung in die Theorie der Elektrosicherheit. Wissenschaftliche Berichte der TH Leipzig 1988, Heft 9, 105 Seiten, ISSN 0138-3809
Siegfried Altmann: Sicherheit elektrotechnischer Betriebsmittel – Eine Entscheidungshilfe für eine quantitative Bewertung. VDE-Fachbericht 50. VDE-Verlag Berlin/Offenbach 1996, S. 43–64
Siegfried Altmann: Elektrosicherheit – Quantitative Bewertungsverfahren. Selbstverlag 2013 und 2014, ISBN 978-3-00-035816-6, Abstracts (deutsch und englisch) mit 105 Seiten, Anlagenband mit 56 eigenen Publikationen, Vertiefungsband (Elektroschutzgüte – Angewandte Qualimetrie) mit 115 Seiten und 26 Anlagen (Inhalte: http://profaltmann.24.eu)/

Einzelnachweise

W. Vesely u. a.: "Fault Tree Handbook." (PDF; 9,49 MB) NUREG-0492, U.S. Nuclear Regulatory Commission, Washington DC 1981 (englisch)
International Electrotechnical Commission [IEC] (Hrsg.): Fault Tree Analysis, IEC 61025. 2. Auflage. 2006, ISBN 2-8318-8918-9.
DIN EN 61025:2007-08, Fehlzustandsbaumanalyse (IEC 61025:2006), Beuth Verlag Berlin, https://dx.doi.org/10.31030/9862300
Clifton A. Ericson: Fault Tree Analysis – A History. (PDF) A History from the Proceedings of The 17th International System Safety Conference. (Nicht mehr online verfügbar.) The Boeing Company; Seattle WA, 1999, archiviert vom Original am 23. Juli 2011; abgerufen am 25. Dezember 2013. Info: Der Archivlink wurde automatisch eingesetzt und noch nicht geprüft. Bitte prüfe Original- und Archivlink gemäß Anleitung und entferne dann diesen Hinweis.@1@2
Simon J. Schilling: Beitrag zur dynamischen Fehlerbaumanalyse ohne Modulbildung und zustandsbasierte Erweiterungen. Dissertation an der Bergischen Universität Wuppertal, 2009 (uni-wuppertal.de [PDF]).
W. Vesely u. a.: Fault Tree Handbook. (PDF; 9,49 MB) NUREG-0492 Page V-3: Component Fault Categories, U.S. Nuclear Regulatory Commission, Washington DC 1981 (englisch)
Military Handbook 217F: Reliability Prediction of Electronic Equipment. (PDF) Abgerufen am 14. März 2019.
Reliability Information Analysis Center: 217Plus. Abgerufen am 4. Dezember 2017.

Weblinks

APIS IQ - Kommerzielles Werkzeug zur Fehlerbaumanalyse (Demoversion verfügbar)
Arbre Analyste - Freie Software zur Fehlerbaumanalyse
BlockSim - Kommerzielles Werkzeug zur Fehlerbaumanalyse
EDRAW - Kommerzielles Visualisierungswerkzeug (Keine Berechnungsfunktion)
ITEM TOOLkit - Kommerzielles Werkzeug (Englischsprachige Seite, Demoversion verfügbar)
Visual-XSel - Kommerzielles Werkzeug zur Fehlerbaumanalyse (Teststellung verfügbar)

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. The authors of the article are listed here. Additional terms may apply for the media files, click on images to show image meta data.

[nasa1-1] W. Vesely u. a.: "Fault Tree Handbook." (PDF; 9,49 MB) NUREG-0492, U.S. Nuclear Regulatory Commission, Washington DC 1981 (englisch)

[iec61025-2] International Electrotechnical Commission [IEC] (Hrsg.): Fault Tree Analysis, IEC 61025. 2. Auflage. 2006, ISBN 2-8318-8918-9.

[din25424-3] DIN EN 61025:2007-08, Fehlzustandsbaumanalyse (IEC 61025:2006), Beuth Verlag Berlin, https://dx.doi.org/10.31030/9862300

[Ericson-4] Clifton A. Ericson: Fault Tree Analysis – A History. (PDF) A History from the Proceedings of The 17th International System Safety Conference. (Nicht mehr online verfügbar.) The Boeing Company; Seattle WA, 1999, archiviert vom Original am 23. Juli 2011; abgerufen am 25. Dezember 2013. Info: Der Archivlink wurde automatisch eingesetzt und noch nicht geprüft. Bitte prüfe Original- und Archivlink gemäß Anleitung und entferne dann diesen Hinweis.@1@2

[schilling-5] Simon J. Schilling: Beitrag zur dynamischen Fehlerbaumanalyse ohne Modulbildung und zustandsbasierte Erweiterungen. Dissertation an der Bergischen Universität Wuppertal, 2009 (uni-wuppertal.de [PDF]).

[nasa2-6] W. Vesely u. a.: Fault Tree Handbook. (PDF; 9,49 MB) NUREG-0492 Page V-3: Component Fault Categories, U.S. Nuclear Regulatory Commission, Washington DC 1981 (englisch)

[milbdbk217f-7] Military Handbook 217F: Reliability Prediction of Electronic Equipment. (PDF) Abgerufen am 14. März 2019.

[217plus-8] Reliability Information Analysis Center: 217Plus. Abgerufen am 4. Dezember 2017.